Introduction

Here we will introduce the notion of a sequence. We start by intuitive approach and explicit definition, then we will show recursive definition and define subsequence

What is a sequence? There are two answers, a precise one and a reasonable one. We start with the former, a formal definition, but if you do not care, just skip to the example below.

Definition.
By a sequence we mean any mapping from the set of natural numbers to the set of real numbers.

Note that we should actually say "real sequences" or "sequences of real numbers", since there are also other sequences; however, these are not covered in the basic calculus course so people usually just say "sequence".

Since such a mapping only accepts positive integers as its argument, it is customary to denote such a sequence in a different way than as a mapping. We can list the values of T as n goes 1,2,3,..., that is, we can write {T(1), T(2), T(3),...}. To emphasize that we have a sequence, instead of T(n) we write a_n, so the whole sequence can be "listed" in the proper order like this: {a₁, a₂, a₃, a₄, ...}, for short we write or {a_n}_n=1,2,3,.... We remark that sometimes we substitute formulas for n in the index and writing it as a lower index could be cumbersome; in such cases we would write a(n) for a_n.

Example: The formulas ,   {2n − 1}_n=1,2,3,...,   or a_n = 2n − 1, n = 1,2,3,... all define the same sequence, sequence that goes {1, 3, 5, 7, 9, 11,...}. Indeed, we have a₁ = 1, a₂ = 3, a₃ = 5, a₄ = 7, etc, so when we put all a_n with n going through natural numbers into a row, it will start 1, 3, 5, 7,...

These three definitions in our example have one thing in common: they provide a formula that allows direct calculation of an arbitrary term of the sequence. For instance, the tenth term of this sequence is a₁₀ = 2⋅10 − 1 = 19.

The other expression for the sequence, the list, is a bit tricky, because it does not specify how the other terms go. Sure, we may guess that the next term after 11 should be 13, but we cannot be sure. So this notation is used only as a supplement, when we want to get some idea how the sequence goes. We can also see much of the behaviour of a sequence by drawing its graph. In our example it is

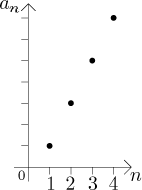
But just like the list, it is not really reliable because we never know for sure what the sequence does after it gets out of our picture. Indeed, both the list and the graph should extend to infinity to capture all terms of this sequence, which is of course impossible. Usually we list or draw just enough terms of the sequence to show the general tendency (if there is any), it is understood that the sequence keeps going (since n keeps increasing, as it runs through all positive integers) in the suggested way.

There is another way to visualise sequences. It may be less useful now but it becomes very handy later, when we start investigating functions. We describe this way in this note.

By the way, if we wanted to define the sequence from our example using the definition, we would use the mapping T(n) = 2n − 1. However, as you saw, when working with sequences, we do not need to refer to the mapping T that formally defines the sequence (also, it is easier not to), so we ignore the formal definition.

Now we are ready to give an intuitive definition:

By a sequence we understand an infinite but countable set of real numbers with a determined order in which these numbers go.

For instance, in our example the sequence is actually all positive odd numbers that are ordered by their size from the smallest. The important thing about a sequence is the values and also their positions. Although we noted above that the list (and the graph) are not reliable for investigating properties of sequences, in fact the list captures the right idea of what a sequence is. The formulas are necessary for precise calculations, but they are just an attempt to write mathematically the idea of the given sequence, and this expression is not unique.

The example {a_n} above was perhaps the most natural way to express the sequence of all odd positive numbers. We remarked that the order is crucial, and it is natural to say that 1 is first, 3 second, 5 the third term and so on. Therefore the indexing a₁ = 1, a₂ = 3, a₃ = 5,... that we had above was natural, then it was just a matter of finding some formula that would make, say, 7 out of n = 4. However, the indexing and the formula are not the only ones. One can, for instance, decide to count the terms as "zeroth, first, second, third,...", that is, to write mathematically b₀ = 1, b₁ = 3, b₂ = 5,...

The sequence given by b_m = 2m + 1, m = 0,1,2,... looks like something very different from the sequence a_n above, but in fact it gives the same sequence: {1, 3, 5, 7, 9,...} (check). The only difference is that in this new mathematical expression, the term 9 has index m = 4, whereas before it had index n = 5. This shows that the important thing is the numbers (the terms) and their order; how we index them and express them in formulas is secondary. The important thing is that the number 9 is a part of the given sequence, comes after 7 and before 11.

One could modify the above formal definition of a sequence to allow other forms of indexing, but this would make it more complicated and most textbooks do not bother. In practice we do not use this formal definiton anyway.

The moral of this story is that the same sequence may have many different descriptions, sometimes it is difficult to even recognize that two descriptions give the same sequence. You should not get too hung up on a particular description, rather focus on the meaning. The list (and the graph) give you some idea about the sequence, and if necessary, this idea can be confirmed using some mathematical description of the sequence. In particular, although the indexing 1,2,3,... is natural, people often use other indexing. The indexing 0,1,2,... above is probably the second most popular (see for instance the geometric sequence and geometric series).

Often we do not even care at which number we start the indexing process. In such a case we would skip references to numbering, because it is understood that for n we put integer numbers starting from a specific one. We then often write just {a_n}.

Here we will show an example of a sequence where we have a good reason to index 2,3,4,... Consider the sequence c_n = 1/ln(n), n = 2,3,4,..., also written for instance in this way: .

Obviously, we cannot substitute n = 1 into this formula. The sequence looks like this:

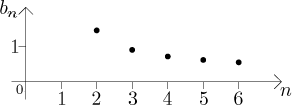
Note that if we wanted, we could have indexed this sequence as m = 1,2,3,..., but then we would have to use the formula 1/ln(m+1). We would get the same numbers in the same order: {1/ln(2), 1/ln(3), 1/ln(4),...}. Note that the graph would change a bit with this new description; it would get shifted to the left by one. This suggests that the graph of this sort is also dependent on indexing, and therefore the exact position of dots in a graph is not exactly important. When a given graph is shifted left or right by some integer distance, the sequence it shows will be still the same, just with different indexing. What is important about these dots is their y-values and their order.

In the above examples we saw the most common way of defining a sequence: by some mathematical formula involving n. This is called the explicit definition. There are other ways. First we will show the "definition" by a list.

Example: {3, π, 2, 2, −1, 0, −1, 0, 2.5,...}, n = 0,1,2,...
We started indexing at 0, so if we use d to denote terms of this sequence, we have d₀ = 3, d₁ = π, and so on. This sequence does not seem to be given by a formula, but it is a sequence nevertheless. Here is its graph:

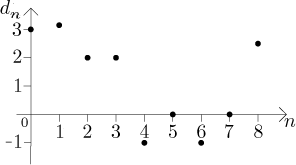
An alternative graph of this sequence can be found in this note

Such definition is rarely seen; the reason is that it actually is not a definition at all. Indeed, we failed to define the whole sequence. For instance, we know that d₈ = 2.5, but we do not know what is d₉. In order to make it into a proper definition, one would have to somehow specify the other terms of this sequence (and there is infinitely many of them, so just a list would not do).

As we already said, list is used as a tool to have an intuitive look at the contents of sequences. Informally it is sometimes used to refer to simple popular sequences, probably the most popular being "1,2,3,..." as a specification of natural numbers, but we should use it sparingly. We should definitely avoid it in formal settings. After all, when we write "the sequence of odd positive integers", it is clear what is meant. On the other hand, when we see {1, 3, 5, 7,...} without any other comment, then we naturally think that the next number is most likely 9, but we cannot be sure. Perhaps the next number is 11, since we could have here the list of all odd positive integers that are not composite numbers.

In the next section we will look at another way to describe sequences, this time a proper one.

Recursive definition works as follows: We give a formula describing how to obtain the next term of the defined sequence assuming that we know the previous ones (this is called a recurrence equation). Of course, one also has to specify necessary first few terms so that the procedure can start.

Example: Our first example of a sequence {2n − 1}_n=1,2,3,... = {1, 3, 5, 7,...} can be also given by these two conditions:
(1)    e₁ = 1,
(2)    e_n+1 = e_n + 2, n = 1,2,3,...

Indeed, the first term agrees, e₁ = a₁. Using the recursive equation (2) with n = 1 gives

e₂ = e₁ + 2 = 1 + 2 = 3 = a₂.

Using the recursive equation with n = 2 gives

e₃ = e₂ + 2 = 3 + 2 = 5 = a₃.

Continuing in this manner, one can check that the first several terms of the two descriptions agree, so one would hope that all are equal. This can be proved by mathematical induction.

We can also try another recursive description of the same sequence:
(1)    g₁ = 1, g₂ = 3, g₃ = 5,
(2)    g_n+1 = 2g_n − g_n−2 − 2, n = 3,4,5,...

Again, the first three terms clearly agree: g₁ = a₁, g₂ = a₂, g₃ = a₃. To check the next, we use the recursive formula (2) with n = 3:

g₄ = 2g₃ − g₁ − 2 = 2⋅5 − 1 − 2 = 7 = a₄.

And so on.

We immediately see the main difference between explicit and recursive definition: The recursive definition does not allow us to calculate directly a desired term of a sequence. Yet every term is uniquely determined (unlike the list notation), so this is also a proper way of defining a sequence. Many sequences can be given both explicitly and recursively, but there is no standard and/or obvious way of passing from one kind of definition to another, there is even no standard way of checking that two descriptions give the same sequence.

Although we usually prefer explicit definition (it is more practical), some sequences can be better expressed recursively and some sequences cannot even be expressed in any other way; sometimes the recursive definition also gives a better insight into the nature of a sequence. Consider the following.

Example: The Fibonacci sequence is given by the equations
(1)    f₁ = 1, f₂ = 1,
(2)    f_n+1 = f_n + f_n−1, n = 2,3,4,...

In words, every term (apart from the first two) is the sum of the previous two. The sequence goes {1, 1, 2, 3, 5, 8, 13,...}. There is an explicit formula for this sequence, but it is exceedingly ugly. Fibonacci (from Pisa, Italy) introduced this sequence in 1202 (in his treatise on arithmetic Liber abaci) to describe the growth of population.

A sequence is an ordered bunch of numbers. Given a sequence, we obtain a subsequence by picking some terms from this sequence and taking them in the original order. For instance, from the sequence {1, 3, 5, 7,...} lichých čísel we can pick a subsequence {1, 5, 7, 13, 137, 345,...}. Or a subsequence {1, 3, 7, 9, 13, 15, 19, 21,...}. Or many others.
Here comes the formal definition:

Definition.
Let {a_n} be a sequence. We obtain a subsequence of this sequence by taking some numbers k₁ < k₂ < k₃ <... from the index set of the given series and considering the sequence .

Example: Consider the sequence a_n = n − 1, n = 1,2,3,..., that is, {0, 1, 2, 3, 4,...}.
Now we pick a subsequence. We choose numbers 1 < 3 < 5 < 7 <... (these are the indices of original terms that will be chosen to form our subsequence) and obtain the subsequence {a₁, a₃, a₅,...}; that is, {0, 2, 4,...}.

Basic properties
Back to Theory - Introduction