In this section we will cover basic examples of sequences and check on their boundedness and monotonicity. We start with alternating sequence and return to it again at the end, we briefly cover arithmetic sequences, but the most important type is the geometric sequence. We return to these examples again in Theory - Limits - Important examples.
An alternating sequence is actually a category, a more general type of a sequence (see the end of this section), but here we will look at the prototype alternating sequence:
![]()
The graph looks like this:
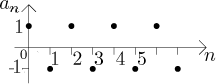
From the picture we immediately see that this sequence is bounded (for all
n we clearly have
It is also possible to index this sequence starting from
This sequence appears quite often; sometimes by itself, more frequently as a part of another sequence; see the last section below.
Definition.
By an arithmetic sequence we mean any sequence of the form
an = a + nd, n = 0,1,2,3,... where a and d are fixed real numbers.
Thus the arithmetic sequence looks like this:
Again, it is possible to index the sequence
Note the following: Every term of an arithmetic sequence can be obtained from the previous term by adding the constant d. For instance,
This is the main idea of the arithmetic sequence. You start with some number
a and then keep adding over and over the same difference d.
Indeed, an arithmetic sequence can be alternatively defined in a
recursive way
like this:
(1)
(2)
It is not difficult to prove by induction that the explicit and recursive definitions define the same infinite sequence.
One last way to characterize an arithmetic sequence: A given sequence is arithmetic if and only if the difference between successive terms is always the same.
Example:
We chose this example to show that the step d can be also negative.
There is a special case when
What are the properties of arithmetic sequences? First we look at the trivial
case of a constant sequence
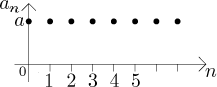
We immediately see that such a sequence is bounded; moreover, it is monotone, namely it is both non-decreasing and non-increasing.
What happens if d is not equal to zero? There are two cases.
Case 1. If
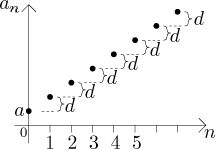
Also, from
Case 2. If
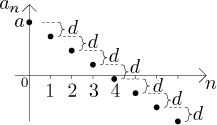
Also, from
Definition.
By a geometric sequence we mean any sequence of the form
an = aqn, n = 0,1,2,3,... where a and q are fixed real numbers.
Thus the geometric sequence looks like this (note that
Again, it is possible to index the sequence
We already saw one example of a geometric sequence, namely the prototype alternating sequence in the beginning.
Note the following: Every term of a geometric sequence can be obtained from the previous term by multiplying it by the constant q. For instance,
a5 = aq5 = (aq4)q = a4q.
This is the main idea of the geometric sequence. You start with some number
and then start multiplying it over and over by the same constant q.
Indeed, a geometric sequence can be alternatively defined in a
recursive way like this:
(1)
(2)
It is not difficult to prove by induction that the explicit and recursive definitions define the same infinite sequence.
One last way to characterize a geometric sequence: A given sequence is geometric if and only if the ratio of successive terms is always the same.
The example that we saw before (the alternating sequence) is somewhat
special, so it is not a good representative of how a geometric sequence
behaves. Another exceptional case is when
To sum it up, the cases
To see what happens when q is a different number we will explore four
typical cases, for simplicity we put (as is customary)
Example:
The choice
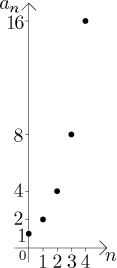
This sequence is increasing, bounded from below (clearly
Example:
The choice

This sequence is decreasing, bounded from below (clearly
These two examples show the basic two types of a geometric sequence, namely
when
Example:
The choice
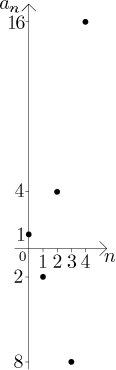
This sequence is not monotone, not bounded from below and not bounded from above, hence not bounded.
Example:
The choice

This sequence is not monotone, it is bounded from below (clearly
For further information see Important examples in Sequences - Theory - Limit.
Note that in the last two graphs we actually just took the graphs of the previous two examples and flipped every second term down around the n-axis. This shows that in investigating sequences with regularly changing signs it may be a good idea to ignore the signs first. This brings us to the last topic.
Our first example was a prototype of an alternating sequence. Now we are ready to look at a more general notion.
Definition.
By an alternating sequence we mean any sequence{an} that is of the forman = (−1)nbn for some non-negative real numbersbn.
By the way, many people would again prefer to start
indexing at some even number so that the alternating sequence starts with
plus; I think that, say,
When investigating an alternating sequence
it is often easier to just ignore the signs and investigate the sequence
In particular, when drawing the graph of an alternating sequence, it is
usually easier to first determine the shape of the graph of
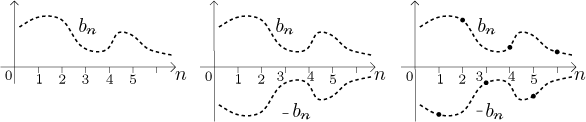
Note that this idea could be also used to draw graphs of sequences whose sign
changes in a regular pattern but not the alternating one. For instance,
Finally, note that there are sequences that not only are not alternating, but
the sign changes do not even follow any pattern; that is, there is no pattern
of signs repeated over and over, and even more, by knowing a certain number
of terms, it is impossible to determine the next sign just by knowing the
signs of those first terms (that is, without explicitly calculating the sign
from the formula). Perhaps the easiest example is