L'Hospitalovo pravidlo

Toto téma je vlastně vypůjčeno z teorie funkcí. Proto jen stručně zopakujeme tuto větu v podobě aplikovatelné na posloupnosti.

Věta (L'Hospitalovo pravidlo).
Nechť f a g jsou funkce definovány na nějakém intervalu (K,∞). Jestliže mají jak f tak g limitu v nekonečnu rovnou 0, nebo jestli jak f tak g mají v nekonečnu nekonečnou limitu, pak

za předpokladu, že limita na pravé straně existuje.

Jak to pomůže? Představme si, že máme dvě posloupnosti, {a_n} a {b_n}, a zkoumáme limitu jejich podílu. Jedním z typických problémů je, že dostaneme neurčitý podíl, neboli typy či . Jestliže vzorec definující posloupnost {a_n} také definuje nějakou funkci f a vzorec definující posloupnost {b_n} také definuje funkci g, můžeme zkusit použít tuto větu. Musíme zkontrolovat, že funkce f a g mají v nekonečnu stejné limity jako dané posloupnosti (obě nula či obě nekonečno). Pokud ano, jsme přesně v pozici citované věty. Můžeme proto přejít na zkoumání funkcí namísto posloupností a použijeme l'Hospitalovo pravidlo.

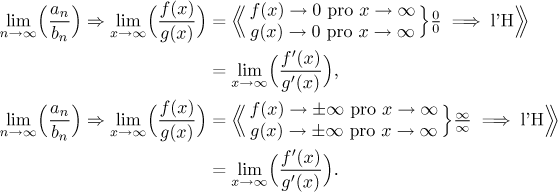
Ať už je to kterýkoliv z těchto dvou případů, pokud limita na pravé straně existuje, pak je tento výsledek také platný pro limitu na levé straně a tedy i pro limitu podílu posloupností. Pokud naopak procedura selže (například pokud limita na pravé straně neexistuje), pak o problému s posloupnostmi nemůžeme nic říct (viz například tento příklad v části Řešené příklady - Limita).

Poznamenejme, že použití l'Hospitalova pravidla obvykle označujeme kratším způsobem, viz další příklad.

Příklad:

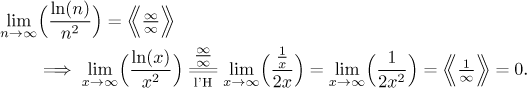
Protože jsme na konci dostali odpověď, ta "podmíněná rovnost" v kroku s l'Hospitalem je ospravedlněna.

Předpoklady věty jsou pro její platnost zásadní. Pokud limita není uvedeného typu, l'Hospitalův vzorec obecně neplatí. Uvažujme následující velice jednoduchý příklad:

Příklad:

Všimněte si, že tento limitní příklad není l'Hospitalova typu (nula dělená nulou, nekonečno dělené nekonečnem, dokonce ani něco dělené nekonečnem) a proto nelze l'Hospitalovo pravidlo použít. Co se stane, když zapomeneme zkontrolovat typ podílu a necháme se svést formou zlomku k použití l'Hospitalova pravidla? Dostaneme špatnou odpověď:

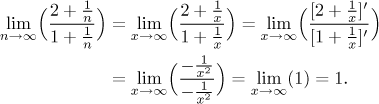
L'Hospitalovu větu lze ve skutečnosti použít i v obecnějších situacích. Verze, kterou jsme citovali, je ta používaná ve většině učebnic a přednášek kalkulu. Proto budeme v Math Tutoru obvykle (když je to možné) předstírat při řešení problémů, že je to jediná verze, kterou známe, takže se doufejme nedostanete do problému tím, že si zde zvyknete používat něco, co váš profák neprobral.

Jak vypadá ta obecnější verze? Případ nelze zobecnit, tam je věta v nejlepší možné verzi. Nicméně v druhém případě, , ve skutečnosti nemusíme mít starosti ohledně čitateli; l'Hospitalovo pravidlo lze také aplikovat na typ "něco děleno nekonečnem"!

Má tato obecnější verze nějakou výhodu? Uvažujme podíl a_n /b_n s b_n→∞. Co se může stát s čitatelem? Pokud jde také do nekonečna, můžeme použít první, populárnější verzi; ta nová tedy není zlepšením. Jestliže a_n konverguje k nějakému reálnému číslu A, pak celý podíl konverguje k A/∞ = 0, takže známe odpověď i bez l'Hospitala.

Jak vidíte, ve většině případů stačí první verze l'Hospitala. Má tedy ta nová verze nějakou výhodu? Rozhodně. Za prvé, jsou problémy, kde sice čitatel do nekonečna jde, ale důkaz tohoto faktu by byl tak pracný, že člověk opravdu ocení, že to nová obecnější verze nevyžaduje (stále je třeba dokázat, že jmenovatel jde do nekonečna, ale to je poloviční práce ve srovnání s první verzí l'Hospitala). Obecnější verze je tedy rozhodně pohodlnější pro problémy s nekonečny (nešetří práci pro problémy typu "nula dělená nulou").
To ovšem není všechno. Může se stát, že čitatel vlastně nejde k žádné limitě! Zatímco první verzi nejde pro typ "neex. děleno nekonečnem" použít, tu obecnější použít můžeme! Ačkoliv jsme tedy slíbili, že se budeme držet té první verze, občas budeme používat i tu obecnější.

Pro praktický pohled na použití l'Hospitalova pravidla viz šuplík "neurčitý podíl" v části Přehled metod - Limita.

V části Řešené příklady - Limita je l'Hospitalovo pravidlo použito v tomto příkladě (což je klasický učebnicový příklad), je také částí většiny ostatních řešení, hlavně v tomto příkladě, tomto příkladě, tomto příkladě, a tomto příkladě. Pro pěkný příklad, na který lze l'Hospitalovo pravidlo použít, ale nevede to k žádnému závěru, podívejte se na tento příklad.

Intuitivní výpočty
Zpět na Teorie - Limita