Intuitivní výpočty

Zde se podíváme na to, jak uhádnout limitu posloupnosti. Tento postup se dá aplikovat na mnoho posloupností a používá několik ingrediencí. Předně je nutno si pamatovat základní limity a algebru limit. Druhou součástí je dobré pochopení vzájemného působení mocnin a exponenciál (a odmocnin). Začneme stručným úvodem.

U mnoha posloupností najdeme součet mocnin a podobných výrazů. Uvažujme například posloupnost {n³ + 5n^1/2 − n⁻²}. První dvě mocniny konvergují do nekonečna (mají kladný exponent), třetí mocninu zapíšeme lépe jako 1/n², což konverguje k 0. Podle algebry limit teď snadno najdeme limitu celé posloupnosti: ∞ + 5⋅∞ − 0 = ∞.

Teď ovšem přijde problém: Jaká je limita posloupnosti {n³ − 5n²}? Víme, že ∞ − ∞ je neurčitý výraz. Existují postupy pro nalezení výsledku, ale příslušné metody často vedou ke komplikovaným výpočům. V této sekci se naučíme, jak uhádnout správnou odpověď a jak ji snadno (více méně) dokázat.

Mimochodem, když sčítáme a odčítáme objekty, či dokonce je násobíme reálnými čísly, jak jsme to dělali v prvním příkladě, říkáme tomu "lineární kombinace". Výraz v prvním příkladě je tedy "lineární kombinace mocnin". Tuto terminologii budeme používat v celé této sekci. Nejprve přesně identifikujeme, jakým typem problému se budeme zabývat.

Všimněte si, že záporné mocniny nezpůsobují v příkladech jako ten výše problémy, viděli jsme, že n⁻² konvergovalo k nule a proto nám nevadilo, když jsme jej v rámci algebry limit přičítali k jiným výrazům. Proto v této sekci budeme uvažovat pouze kladné mocniny. Když se stane, že jsou mocniny přímo přirozená čísla, tak vlastně máme polynomy. Zde ale budeme pracovat mnohem obecněji a povolíme také kladné exponenty, které nejsou celá čísla (například exponent 1/2 neboli odmocnina).

Povolíme také "exponenciály", mocniny typu eⁿ, 2ⁿ atd. A protože zase víme, že qⁿ→0 jestliže |q| < 1 a 0 není problém v součtech, budeme pouze uvažovat exponenciály qⁿ s |q| > 1.

To ale není všechno. Zatímco "lineární kombinace" mocnin a exponenciál (mocniny/exponenciály násobené čísly a pak sečtené/odečtené) se objevují často, povolíme ještě i jiné výrazy: logaritmy, faktoriály a dokonce i mocniny typu nⁿ. Teď jsme připraveni formulovat otázku, kterou se tu snažíme řešit:

Otázka:
Máme výraz ve tvaru α⋅A(n) + β⋅B(n) +..., kde funkce A(n), B(n),... mohou být mocniny n^a s a > 0, exponenciály qⁿ s |q| > 1, mocniny logaritmů [ln(n)]^a s a > 0, faktoriály jako n! a obecné mocniny jako nⁿ. Co se stane s tímto výrazem, jestli necháme n jít do nekonečna?

Všimněte si, že všechny výrazy vypsané výše jdou do nekonečna pro n→∞. Když se dají dohromady prostřednictvím lineární kombinace, dostaneme v typickém případě neurčitý výraz s nekonečny, protože výsledek doustaneme pouze v případě, že jsou všechna nekonečna sečtená. Brzy uvidíme, že některá nekonečna jsou "větší" a důležitější než jiná.

Řešení problému:
Jestliže necháme n→∞, pak se výraz výše specifikovaného typu bude chovat přesně jako jeho dominantní člen. Matematický důkaz se udělá tak, že se vytkne dominantní člen z výrazu a pak se aplikuje limita, výraz, který vznikne po vytknutí, by měl konvergovat k reálnému číslu.

Dominantním členem myslíme člen, který pro velká n převáží zcela nad ostatními členy lineární kombinace, takže je možné je ignorovat, nebudou mít vliv na tendenci, kterou má dominantní člen okolo nekonečna. Mezi typy uvedenými výše (mocniny, exponenciály, logaritmy,...) existuje hierarchie. Když řekneme "člen A převáží nad členem B pro velké hodnoty n", pak tím míníme, že když zkoumáme limitu výrazu α⋅A + β⋅B pro n jdoucí do nekonečna, tak můžeme člen B ignorovat a jen se zabývat členem A. Pro hlubší náhled do tohoto srovnávání nekonečen klikněte sem.

Příklad:
Brzy uvidíme, že n² převáží nad ln(n). Teď si předstame, že potřebujeme najít limitu posloupnosti {23ln(n) − n²}. Když se n stane opravdu velkým, druhý člen převáží a ten první můžeme ignorovat. Celá posloupnost se tak bude chovat (když n roste do nekonečna) jako posloupnost {-n²}, o které víme, že konverguje do mínus nekonečna. Následně také daná posloupnost jde do mínus nekonečna.

Tento výsledek je samozřejmě jen hádání. Napsali jsme výše (v Řešení), že matematicky to můžeme udělat vytknutím dominantního členu. Zkusíme to:

Ten první člen teď jasně konverguje do nekonečna. Co dělá ta část v závorce? Zlomek je typu nekonečno dělené nekonečnem, který je řešen pomocí l'Hospitalova pravidla. Úžasnou shodou okolností jsme zrovna tento problém řešili v předchozí sekci L'Hospitalovo pravidlo, takže víme, že konverguje k nule. Můžeme tedy dokončit problém:

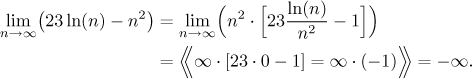
Všimněte si, že zlomek, který se objevil po vytknutí dominantní mocniny, opravdu konvergoval k reálnému číslu, přesně jak jsme předtím tvrdili.

Existuje způsob, jak zapsat korektně nejen ten správný matematický výpočet, ale i naše intuitivní vývody. Když napíšeme A(n) ∼ B(n), míníme tím, že výrazy A a B se chovají stejně pro n→∞; z praktického pohledu jsou výrazy A(n) a B(n) stejné, když se n stane opravdu velkým. Někdy se také říká, že a a B jsou "stejného řádu". Náš intuitivní výpočet nahoře se dá zapsat následovně:

23ln(n) − n² ∼ −n²→−∞.

Je důležité si uvědomit, že tento způsob zápisu není univerzálně přijímán. Také nepředstavuje správné řešení - konec konců, jen jsme stejně hádali. Každá odpověď, kterou tímto způsobem dostaneme, se musí potvrdit matematickým výpočtem, například tou vytýkací procedurou předvedenou výše.

Když se díváme na mocniny v lineární kombinaci mocnin a podobných členů, děláme vlastně dvě rozdílné věci. Nejprve se podíváme jen na samotné mocniny, exponenciály a podobně, ve smyslu že ignorujeme konstanty, kterými jsou násobeny. Tímto způsobem určujeme typ výrazu. Například výraz "13⋅[ln(n)]³" je typu [ln(n)]³ a poslední příklad byl typu n², protože typ výrazu je dán typem dominantního prvku. Typ nám řekne, jak se daný výraz chová, když se n stane opravdu velkým.

Tento typ se používá, když se zhruba porovnává chování rozdílných výrazů, zjišťuje se, které se dají ignorovat a podobně. Ale pak, když začneme opravdu odhadovat, jaká je limita v nekonečnu, musíme vzít násobící konstanty v úvahu. Takže sice řekneme, že 23ln(n) − n² je typu n² když se n stává velkým, ale když hledáme limitu, tak musíme říct, že se chová jako -n², tedy musíme započítat konstanty při proceduře používající ∼. K tomuto tématu se za chvíli vrátíme.

Jak vidíte, tato intuitivní procedura může být jednoduchá, správný zápis (matematický) může být občas delší, ale neměl by nikdy být zákeřný, pokud tedy správně identifikujeme a vytkneme dominantní člen. Což nás přivádí k hlavní části této sekce:

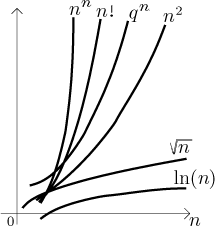
Zde je seznam výše jmenovaných výrazů v pořadí od nejvíce dominantnímu k nejméně dominantnímu. Každý vypsaný výraz převažuje nad výrazy vypsanými dále:

(1)   mocnina nⁿ,
(2)   faktoriál n!,
(3)   exponenciála qⁿ for |q| > 1,
(4)   mocnina n ^a for a > 0,
(5)   logaritmus [ln(n)]^a for a > 0.

Při praktickém použití lidé často používají lidovější způsob, jak si pamatovat tuto hierarchii, pomocí frází jako "mocniny přebijí logaritmy" a "exponenciálny přebijí mocniny" atd.

Když zkoumáme lineární kombinace takovýchto členů, vždy nejprve nalezneme dominantní výraz. Může se tam ovšem výrazů této kategorie vyskytovat více, musíme proto také vědět, jaká je vnitřní hierarchie uvnitř každé kategorie. Zde je pravidlo jednoduché: U typů (3), (4) a (5) je vždy nějaký parametr (a či q) a ten nejvyšší je dominantní.

Připomeňme, že když q < −1, pak {qⁿ} nemá limitu. Když tedy takovýto člen převáží v lineární kombinaci, pak tato kombinace nemá limitu. Když se porovnávají mezi sebou exponenciály, o dominanci rozhoduje absolutní hodnota |q|.

Problém dominance je vlastně jednou z možných odpovědí na otázku "které nekonečno je větší". rotože pro q < −1 nemáme qⁿ→∞, budeme teď uvažovat pouze q > 1. V následujícím obrázku (ne zcela v přesném měřítku) zkusíme symbolicky vyjádřit vzájemný vztah rozličných výrazů, čímž obdržíme škálu mocnin:

Příklad:
Jaká je limita výrazu {13⋅2ⁿ + n² − 5⋅3ⁿ − ln(n)^1/2}?

Řešení: Jsou zde tři kategorie: exponenciály, mocniny a logaritmy. Exponenciály jsou na seznamu nejvýše, proto dodají dominantní člen. Jsou dva kandidáti, 2ⁿ a 3ⁿ. Protože 3 > 2, ta druhá exponenciála je dominantní, daný výraz je typu (či řádu) 3ⁿ. Můžeme tedy ignorovat ostatní členy a tipujeme, že

13⋅2ⁿ + n² − 5⋅3ⁿ − ln(n)^1/2 ∼ −5⋅3ⁿ→−5⋅∞ = −∞.

Jak tento výsledek potvrdíme matematicky? Vytknutím dominantního členu.

Ty tři zlomky v závorce je nejlepší udělat zvlášť. První je jen geometrická posloupnost, druhé dva vedou na l'Hospitalovo pravidlo poté, co změníme zápis z posloupností na funkce:

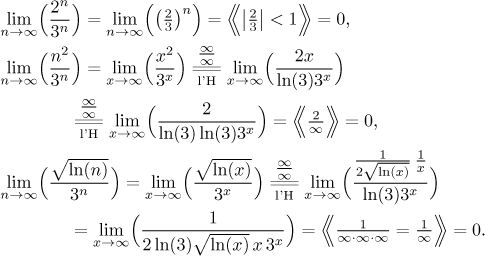
Nakonec tedy dostaneme

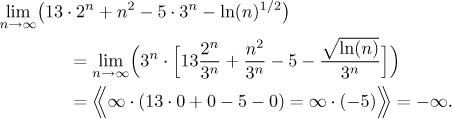
Poznamenejme, že tento postup často aplikujeme i na výrazy, které nevypadají zcelajako ty uvedené výše, ale dají se na ně převést algebraicky. Dva nejtypičtější příklady jsou (2n)³ = 2³⋅n³ = 8⋅n³ a 3²ⁿ⁺¹ = (3²)ⁿ⋅3¹ = 3⋅9ⁿ.

Popsaný intuitivní postup také funguje, pokud jsou ve výrazu odmocniny, neboli pokud jsou některé části výrazu skryty pod odmocninami. Postupujeme pak následovně. Nejprve individuálně prozkoumáme každou odmocninu. Vždy určíme dominantní člen výrazu pod odmocninou, ten určí typ výrazu pod odmocninou. Když na tento člen aplikujeme příslušnou odmocninu, dostaneme typ celé odmocniny jako celku. Toto se dá potvrdit vytknutím, zbylá odmocnina pak musí mít vlastní limitu v nekonečnu.

Po zvládnutí všech odmocnin (pokud nějaké jsou) pak dáme všechny typy dohromady (ty samostatné i ty zastupující odmocniny) a určíme dominantní člen celého výrazu. Tento postup je někdy třeba vícekrát opakovat, v případě že se vyskytuje odmocnina, pod kterou je výraz s další odmocninou a tak podobně. Nakonec, až máme dominantní člen celégo daného výrazu, už postupujeme jako předtím; vytkeme jej z dominantního výrazu a určíme limitu.

Poznámka: Vytýkání je většinou jednodušší, pokud při něm jakoby opakujeme tu hádací proceduru; takže nejprve vytkneme dominantní členy z odmocnin a pak se postupně propracujeme úplně ven s dominantním členem celého výrazu.

Příklad: Najděte (jestli existuje)

Nejprve se podíváme na odmocninu. Pod ní jsou jen mocniny, jsou tedy ve stejné kategorii a největší mocnina vyhraje. V našem případě je výraz pod odmocninou typu n⁶. Když teď na něj aplikujeme odmocninu, zjistíme, že odmocnina jako taková je typu n^6/2 = n³, stejně jako druhá část daného výrazu. Máme tedy dva členy stejného typu, dva dominantní členy, a tedy nemůžeme žádný z nich ignorovat. Zkusíme teď tedy hádat, začneme tím, že ignorujeme člen pod odmocninou, o kterém víme, že to jde.

Získali jsme kýžený odhad (a cestou jsme viděli, že odmocnina se opravdu chová jako 3n³ pro velkán) a teď jej dokážeme. Začneme vytknutím z odmocniny, přesně jak bylo doporučeno.

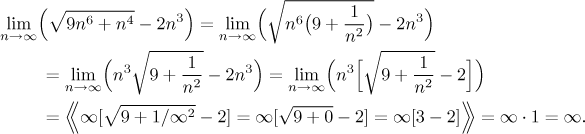
Teď se dostáváme k zajímavé věci. To hádání výsledku mohlo vlastně být špatně a ani bychom o tome nevěděli, protože jsme ještě neprobrali důležitou věc. Zatím jsme měli štěstí, ale teď je čas na

Varování: Co se stane, když je více diminantních členů? Pokud se sčítají, dá se to udělat bezpečně. Pokud se ovšem odčítají (jinými slovy, pokud by algebra limit vedla na neurčitý tvar ∞ − ∞), pak musíme být obezřetní. Pokud by normální algebra aplikovaná na dominantní členy během hádání zachovala tento dominantní člen, tak ti můžeme udělat. Pokud by algebra způsobila, že tento dominantní člen zcela zmizí, nesmíme tento krok udělat!

Pokud bychom například měli v posledním příkladě 4n⁶ namísto 9n⁶, pak by se odmocnina chovala jako 2n³, což by se zkrátilo s tím druhým členem. ptoto bychom nemohli udělat krok 2n³ − 2n³ = 0.

Jaký je pro to důvod? Protože když hádáme, každý člen vlastně nereprezentuje jen sebe, ale možná také spoustu dalších členů nižší důležitosti, které jsou v něm schovány (např. ta část "+n⁴" v posledním příkladě). Když odečteme dominantní členy a ještě nějaký zbyde, pak ty části, které jsme ignorovali předtím, mohou být stále ignorovány (dominantní člen, který je předtím zastínil, tam ještě pořád je) a hádání je tak správné. Kdyby nicméně algebra vedla ke zmizení dominantního členu, pak by jeden ze členů, které jsme předtím ignorovali, byl náhle povýšen k dominanci a rozhodoval by o výsledku limity! Ta rozhodně nemusí vyjít nula, jak dostaneme po krácení dominantních členů. V takovémto případě je tedy třeba udělat přesnější a opatrnější výpočet, který neignoruje členy, které jsou přechodně nezajímavé.

Srovnejte následující dva příklady. Asi vám budou připadat trochu srandovní, ale dobře ilustrují podstatu věci. U každého z nich budeme nejprve hádat (i kdyby to bylo špatně) a pak správný výpočet. V prvním příkladě je hádání správně; všimněte si, že ve vlastním výpočtu se po sečtení členů dá pořád ignorovat člen "+n", takže opravdu nehraje roli v konečném výsledku. V druhém příkladě je člen n povýšen do dominantní pozice.

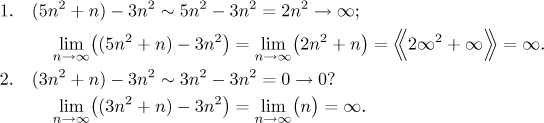
Pravidlo pro dominantní členy:
Pokud hledáme limitu hádáním a ve výrazu je více dominantních členů, můžeme je dát dohromady pouze v případě, že se ve výsledku nevykrátí.

Pokud ke krácení dojde, musíme se vzdát intuitivních výpočtů a zkusit jiné metody. Nicméně i pak může hádání pomoci jako příprava k jinému řešení, protože často je užitečné znát typy výrazů v posloupnosti. Jeden příklad lze nalézt v části Řešené příklady - Limita.

Teď jsme se dostali k nejobecnějšímu typu, který se dá řešit intuitivním výpočtem: zlomku, jehož čitatel a jmenovatel jsou typu, který jsme měli výše. Jak se s takovými zlomky vypořádáme? Nejprve zvlášť prozkoumáme čitatel a jmenovatel: Určíme dominantní členy a vytkneme je. Máme tak jeden dominantní člen v čitateli a jeden ve jmenovateli, takže je zkrátíme, pokud to jde, a najdeme limitu výsledného zlomku. I tady může pomoci škála mocnin. Jestliže preváží člen v čitateli, dostaneme nekonečnou limitu. Pokud převáží člen ve jmenovateli, dostaneme nulu.

To je vlastně docela přirozené. Obvykle dostáváme situaci nekonečna děleného nekonečnem, a převážení znamená, že jedno nekonečno je větší než to druhé, takže vyhraje. Například pokud nekonečno ve jmenovateli převáží nad nekonečnem v čitateli, znamená to, že jmenovatel je nakonec mnohem a mnohem větší než čitatel a výsledný zlomek je velice malý, což naznačuje, že zlomek jde k nule.

Zmínili jsme, že někdy je možno dominantní členy čitatele a jmenovatele zkrátit po vytknutí; dostaneme pak typ (či řád) zlomku jako celku.

Někdy v případě zlomku lidé dávají přednost krácení před vytýkáním a porovnáváním. Funguje to - ale jen někdy. Důkladná diskuze ohledně zlomků polynomů je v této poznámce.

Příklad:
Najděte (pokud existuje)

Nejprve se pokusíme odpověď intuitivně uhádnout, pak to uděláme pořádfným výpočtem. Měli bychom začít s odmocninami.

Ve třetí odmocnině je dominantním členem třetí mocnina, pro velké hodnoty n tedy můžeme ostatní členy ignorovat. Ve druhé odmocnině ve jmenovateli převládne exponenciála nad druhou mocninou, a tak tuto mocninu můžeme ignorovat.

Teď známe typy odmocnin, můužeme je tedy srovnat s ostatními členy a najít dominanty, zvlášť v čitateli a jmenovateli. Pak použijeme hierarchii mocnin k odhadnutí výsledku.

Jak jsme uvažovali? V čitateli mocniny přebijí logaritmy, a největší mocnina je druhá mocnina. Mimochodem, toto ukazuje, proč je důležité začít vždy odmocninami. Na první pohled by se totiž mohlo zdát, že n³ je v čitateli dominantou, ale po analýze odmocniny jsme viděli, že se to vlastně chová jen jako n.

Ve jmenovateli byla dominantní exponenciála 2ⁿ, takže jsme ignorovali zbytek. Nakonec jsme použili toho, že exponenciály přebijí mocniny, a dospěli k závěru, že zlomek konverguje k nule.

Teď bychom měli potvrdit náš odhad výpočtem - jmenovitě vytknutím. Ačkoliv by to zkušený student zvládl na pár řádcích, dáváme přednost ukázat více detailů a přidáme také poznámku ohledně těch dvou odmocnin; nabízíme proto výpočty zde.

Intuitivní výpočty je také možné aplikovat na komplikovanější výrazy. Zlomek typu popsaného výše je možno zavřít pod odmocninu a pak přičten k dalším mocninám, exponenciálám atd. Je těžké napsat přesně, na jaké výrazy je možné tento postup aplikovat, ale trochu nepřesně to vypadá takto: Základním stavebním kamenem je lineární kombinace mocnin, exponenciál, mocnin logaritmů, faktoriálů a obecných mocnin (jejich násobky jsou sčítány/odečítány). Tato základní kombinace může být uzavřena pod odmocninu, čímž vzniká další stavební cihla, která může bvýt dále použita v jiné lineární kombinaci. Takové lineární kombinace lze kombinovat do zlomku, a tyto procedury mohou být v libovolném pořadí opakovány.

Varování: Ignorování členů je možné pouze v základních lineárních kombinacích, tj. součtech s mocninami, exponenciálami, mocninami logaritmů, faktoriály a obecnými mocninami. Další výrazy (jao odmocniny, zlomky) mohouá být ignorovány pouze poté, co jsou nahrazeny svými dominantními členy a stanou se tak legitimními členy lineárních kombinací. Není možné ignorovat členy ve výrazech, které nejsou součástmi odmocnin či zlomků, ale jsou zamíchány do jiných výrazů. Například můžeme nahradit výraz n − ln(n) pouhým n v případě, že je tento výraz pod odmocninou nebo je to část zlomku, ale nemůžeme to už udělat, pokud je to řekněme v argumentu exponenciály. Například snadno ukážeme, že 2^{n − ln(n)} ∼ 2ⁿ je špatně, a bez dalšího zkoumání nevíme, zda platí ln(n − ln(n)) ∼ ln(n) nebo arctg(n − ln(n)) ∼ arctg(n).

Pro mnoho příkladů odkazujeme na část Řešené příklady - Limita.

Ačkoliv se to nestává často, někdy jsou výrazy výše popsaného typu vynásobeny navzájem. V takovém případě se intuitivní procedura aplikuje na každý člen součinu a u každého se najde jeho typ. Typ celého součinu je pak dán součinem typů jednotlivých členů. Obvykle se ovšem takto nedostane jeden z typů, které jsme probrali (mocniny, exponenciály atd.), spíše součin takových typů. Takové výrazy nejsou vypsána v naší škále mocnin, takže zřídka získáme tímto zpúsobem konečné odpovědi. Často lze nicméně využít zkušenost s typy k získání užitečného náhledu.

Příklad:

Všimněte si, že jsme zjistili, že čitatel je typu n2ⁿ a jmenovatel je typu n²n!; naštěstí jsme dokázali zkrátit a tak našli odpověď pomocí škály mocnin. Stačí ovšem udělat malou změnu a už to nebude fungovat:

Nyní srovnáváme (po zkrácení) dva typy, n2ⁿ v čitateli a n! ve jmenovateli. Protože ten první výraz není součástí obvyklé škály mocnin, takže nevíme, co se stane, když se tyto dva typy vydělí. Víme, že n! pobije 2ⁿ, ale n2ⁿ evidentně utíká do nekonečna mnohem rychleji než jen 2ⁿ; je možné, aby to rostlo o tolik rychleji, aby to dokonce přerostlo n!, to jest je možné, aby n2ⁿ přebilo n! ?

Odpověď zní: ne. Ve skutečnosti je n2ⁿ nový typ, který převáží nad 2ⁿ ale je přebyt n!, takže je přesně mezi těmito dvěma typy. Daná posloupnost tedy konverguje k nule; důkaz je vlastně jen modifikací důkazu, že faktoriály přebijí exponenciály.

Stolz-Cesaro theorem
Zpět na Teorie - Limita