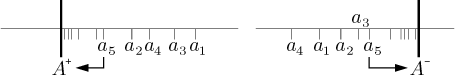Algebra limit (s nekonečnem)
Zde máme seznam algebraických výrazů, které lze použít při výpočtu limit. Jde
vlastně o rozšíření obvyklé algebry. Také se zde zmíníme o neurčitých
výrazech. Ty jsou blíže probrány
zde. Určitě se podívejte na
Poznámky na konci, ať správně chápete vypsaná pravidla, hlavně se podívejte
na poslední poznámku. Pokud vás zajímá jen shrnutí,
zde najdete stručný výpis algebry
limit.
Sčítání/odčítání:
Reálná čísla se sčítají/odčítají jako obvykle.
Nekonečno se ve většině případů chová rozumně:
∞ ± L = ∞
pro všechna reálná čísla
L,
∞ + ∞ = ∞.
Neurčitý výraz:
∞ − ∞.
Násobení/dělení:
Reálná čísla se násobí jako obvykle, také dělení funguje normálně pokud
je jmenovatel nenulový.
1/0+ = ∞
a
1/0- = −∞,
kde 0+ zastupuje posloupnost konvergující k
nule, jejíž členy jsou všechny kladné, a 0- zastupuje posloupnost
konvergující k nule, jejíž členy jsou všechny záporné (vlastně stačí mít tu
kladnost/zápornost jen na "konci" posloupnosti, tj. po vynechání "začátku",
konečného počtu členů posloupnosti). Viz poznámka na konci.
Nekonečno se chová pěkně v následujících případech:
∞⋅L = ∞
a
∞/L = ∞
pro všechna kladná L,
∞⋅L = −∞
a
∞/L = −∞
pro všechna záporná L,
L/∞ = 0
pro všechna reálná čísla L,
∞⋅∞ = ∞.
Neurčité výrazy:
∞⋅0,
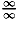 a
a
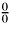 .
.
Výrazy L/0 pro nenulové L a
∞/0
nebývají zahrnovány mezi neurčité výrazy, ale patří
tam, protože mohou dát tři rozdílné odpovědi:
∞,
−∞ a
"neexistuje". Pro detaily konzultujte Poznámky níže.
Mocniny:
Reálná čísla pracují v mocninách jako obvykle; mimo jiné to znamená, že
mocnina AB funguje jako obvykle pro kladné A.
Když A kladné není, je třeba být opatrný, například 00
je neurčitý výraz (viz dále).
Nekonečno se chová pěkně v následujících případech:
∞L = ∞
pro všechna kladná L,
∞L = 0 pro všechna záporná L,
L∞ = ∞
jestliže L > 1,
L∞ = 0
jestliže |L| < 1, a
L∞ neex. jestliže
L < −1,
L−∞ = 1/L∞ = (1/L)∞,
takže
L−∞ = 0
jestliže |L| > 1,
L−∞ = ∞
jestliže 0 < L < 1, a
L−∞
neex. jestliže
−1 < L < 0.
∞∞ = ∞.
Neurčité výrazy:
1∞,
00,
∞0.
Některé elementární funkce:
e∞ = ∞,
proto také e−∞ = 1/e∞ = 1/∞ = 0.
ln(∞) = ∞ a
ln(0+) = −∞,
kde 0+ zastupuje posloupnost konvergující k nule,
jejíž členy jsou všechny kladné (či alespoň kladné až na konečný počet
vynechaných členů).
arctg(∞) = π/2,
arctg(−∞) = −π/2.
Poznámky
Poznámka o významu algebry limit a neurčitých věcech
Ve výše vypsaných rovnostech libovolný daný symbol nezastupuje opravdové
číslo; spíše symbolizuje posloupnosti s limitou rovnou tomuto symbolu.
Například 2⋅3 = 6 v tomto kontextu nehovoří o reálných
číslech, ale znamená to: "Když je posloupnost konvergující k 2 vynásobena
posloupností konvergující k 3, výsledná posloupnost konverguje k 6." To
vysvětluje, proč někdy algebra limit selže v případech, které by se zdály
jasné, kdybychom pracovali s reálnými čísly. Například jedna na libovolnou
mocninu je jedna, ale jedna na nekonečno je neurčitý výraz. Proč?
Jedna na nekonečno je ve skutečnosti zkratka pro posloupnost konvergující k 1
umocněnou na posloupnost, která konverguje k nekonečnu. Protože tato operace
se dělá člen po členu, obdržíme posloupnost mocnin
{an bn},
kde základy an jsou nakonec blízko k 1, ale nemusí
být přesně jedna. Mohou být například všechny trochu větší než 1. Protože
jsou umocněny na velká čísla (exponenty bn jdou do
nekonečna), mohou dávat velké výsledky a vzniklá posloupnost může klidně
konvergovat do nekonečna. Vše záleží na rovnováze. Jestliže se exponenty
stanou opravdu velkými dřív, než mají základy příležitost se přiblížit k 1,
pak "1 na nekonečno" může být velké číslo. Naopak pokud se základy přiblíží k
1 velice rychle, zatímco exponenty se do nekonečna loudají, pak blízkost bází
k 1 může převážit nad růstem exponentů a "jedna na nekonečno" múže být blízké
k jedné.
Podobně pokud jsou báze menší než jedna a jdou k jedné pomalu, zatímco
exponenty se zvětšují velice rychle, pak "jedna na nekonečno" může být velice
malé, dokonce i nula.
Podobná rovnováha rozhoduje o výsledku dalších neurčitých výrazů, například
výsledek
∞ − ∞
záleží na tom, které nekonečno roste rychleji.
Poznámka o 1/0
Stačí prozkoumat 1/0, protože výrazy L/0 a nekonečno dělené nulou se
chovají stejným zpúsobem. Základní myšlenka je, že jedna dělená velice malým
číslem dá velice velké číslo, jehož znaménko záleží na znaménku dělitele.
Protože u malých čísel je od kladného k zápornému jen malá změna, vyplývá z
toho, že taková malá změna ve jmenovateli způsobí ohromnou změnu ve výsledku:
velký výsledek změní znaménko (například
1/0.0001 = 10,000, zatímco
1/-0.0001 = −10,000).
Připoměňme, že "0" zastupuje určitou posloupnost
{an} konvergující k nule. Hodnota
1/0 záleží na
znaméncích an. Jestliže jsou všechna
an kladná (což značíme 0+ v algebře
limit, ve skutečnosti stačí, aby byly členy kladné po vynechání konečného
počtu na začátku), znamená to, že vždy dělíme "téměř jedna" (připomeňme, že
"1" zastupuje nějakou posloupnost bn konvergující k
1) malými kladnými čísly, obdržíme tak velká kladná čísla. Výsledná limita by
tedy měla být nekonečno. Jestliže jsou naopak všechna
an záporná
(což značíme 0- v algebře limit, ve skutečnosti stačí, aby byly
členy záporné po vynechání konečného počtu členů na začátku), znamená to, že
dělíme "téměř jedna" malými zápornými čísly a dostáváme tak záporná čísla,
která jsou v absolutní hodnotě velice velká. Výsledná limita by tedy měla
být mínus nekonečno. Tímto způsobem obdržíme ty dva vzorce pro 1/0
v naší algebře limit:
1/0+ = ∞
a
1/0- = −∞.
Třetí alternativa je, že jak jdeme podél posloupnosti
an k jejímu konci, žádné znaménko nepřeváží; jinými
slovy, jakkoliv daleko v posloupnosti dojdeme, vždycky jsou ještě dál kladná
i záporná an. Dá se to také vyjádřit následovně:
Není možné zajistit, aby měla posloupnost stejné znaménko, pomocí odříznutí
jejího začátku, tj. vypuštěním konečného počtu členů. Protože posloupnost
an jde k nule a bn je pro
velká n přibližně jedna, čísla
bn /an v absolutní
hodnotě jdou do nekonečna, ale znaménko se nepřestává měnit nějakým způsobem
z kladného v záporné a zpět; výraz
bn /an tak dává
oscilující posloupnost, kde velikost oscilace roste. V takovém případě
dostaneme výsledek, že limita posloupnosti
bn /an neexistuje.
Závěr je, že když vidíme typ 1/0, musíme prozkoumat znaménko posloupnosti ve
jmenovateli. Pokud zjistíme, že určité znaménko nakonec převáží, můžeme
použít algebru limit. Pokud zjistíme, že žádné znaménko nepřeváží a pořád se
mění, pak odpověď je, že limita neexistuje. Pokud nejsme schopni znaménka
vyšetřit, musíme tento konkrétní případ 1/0 vzdát.
Pokud chcete vidět nějaké příklady tohoto chování, podívejte se na
neurčité výrazy.
Důležitá poznámka o jednostranných limitách
V této poznámce dáme dohromady myšlenky z předchozích dvou poznámek, abychom
vysvětlili, proč někdy potřebujeme uvažovat jednostranné limity.
To, že číslo v algebře limit není přesně to číslo, ale symbol pro
konvergentní posloupnost, nám umožňuje dělat věci, které bychom s čísly
dělat nemohli. Víme například, že nelze dosadit číslo 0 do funkce
1/x2. V algebře limit nicméně máme
1/02 = ∞
(skoro, jak ještě vysvětlíme). Proč? 0 zastupuje posloupnost
{an} konvergující k nule. Jestliže tato posloupnost
splňuje podmínku, že an jsou nenulové, pak
an2 jsou kladná čísla konvergující k
nule, tudíž 1/an2 musí jít do nekonečna.
Můžeme vlastně napsat 02 = 0+ a použít
výsledek z předchozí poznámky.
Někdy při pokusu o dosazení konvergentní posloupnosti do funkce musíme být
opatrní a trochu víc pracovat. Jaký je například výsledek
ln(0)? Připomeňme,
že logaritmus je definován jen pro kladná čísla, takže zde je třeba se
podívat blíže na posloupnost {an} reprezentovanou
tou "0". Aby měl výraz smysl, její členy musí splňovat
an > 0. Pak mohou být dosazeny do
logaritmu a ln(an) jde do
−∞.
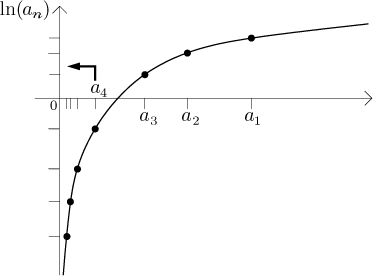
Posloupnost jsme označili na reálné ose, hodnoty
ln(an) se objevují na svislé ose.
Pro takovou "0" jsme měli značení, v předchozí poznámce jsme jí říkali
0+, a právě jsme odvodili, že
ln(0+) = −∞.
Tyto úvahy se vyskytují docela často a zasluhují si formální definici.
Definice (jednostranné limity)
Nechť {an} je posloupnost konvergující k
reálnému číslu A.
Jestliže
an > A pro všechna n,
pak řekneme, že {an} konverguje k A zprava.
Značíme to
an→A+,
v algebře limit pro takovou
posloupnost používáme symbol A+.
Jestliže
an < A pro všechna n,
pak řekneme, že {an} konverguje k A zleva.
Značíme to
an→A-,
v algebře limit pro takovou
posloupnost používáme symbol A-.
Následující obrázku ukazují, jak jednostranné limity vypadají.
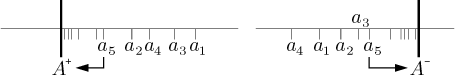
Viděli jsme dva nejtypičtější příklady, u kterých jsou jednostranné limity
užitečné, výrazy 1/0 a ln(0). Kdykoliv dostanete tyto výrazy, měli byste
vyšetřit, zda je ta 0 jednostranná, jinak není možné dělat žádné závěry.
Takových příkladů je více. Pokaždé, když zkusíte dosadit nějaké A do
funkce a objeví se problém, měli byste se zeptat, jestli by situaci pomohlo,
kdybyste věděli, že je A jednostranné.
Příklad: Jaký je výsledek
tg(π/2)?
Víme, že tangens není v
π/2
definován, což ukazuje, že je třeba dále pátrat. Protože víme, jak tangens
vypadá,
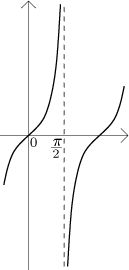
vidíme, že to je přesně situace, kde mohou jednostranné limity pomoci. Když
si představíme příklady posloupností konvergujících k
π/2 zprava a zleva,
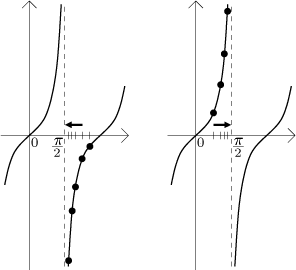
měli bychom být schopni odhadnout správný výsledek:
tg((π/2)+) = −∞,
tg((π/2)-) = ∞.
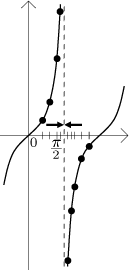
Když se tedy potkáte s výrazem
tg(π/2),
pak je třeba zjistit víc o posloupnosti uvnitř tangensu. Pokud
je její limita jednostranná, je výsledek jak jsme právě napsali. Pokud
posloupnost nepřestává přeskakovat napravo a nalevo od
π/2, pak limita neexistuje.
![]() a
a
![]() .
.