Here we will look at the most important examples of sequences. We will focus on their convergence, we will also remark on boundedness and monotonicity of sequences that are introduced for the first time here. After alternating and arithmetic sequences we look at geometric sequence, then we look at powers, factorial, the exponential, and finally sine and cosine.
As we saw before, the
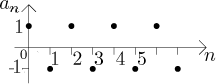
prototype alternating sequence

Just by looking at the graph we see that this sequence does not have a limit. This is the simplest example of an oscillation-type problem preventing the existence of a limit.
The behaviour of the arithmetic sequence
If
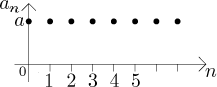
From the picture it seems clear that this sequence is convergent, and indeed we have
![]()
If
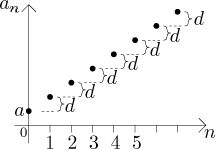
Such a sequence is divergent, but the limit exists and is equal to infinity;
that is,
If
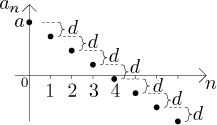
Again, such a sequence is divergent, but the limit exists and is equal to
negative infinity; that is,
The behaviour of the geometric sequence
For other values it is good to recall the four examples that we saw in
Theory - Introduction -
Important examples. They represented four alternatives that can happen
if
Case 1:
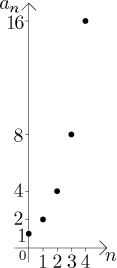
In this case the sequence diverges, but has a limit, namely infinity (see the end of the note here).
Case 2:

and when

from the point of view of convergence it is the same case: the sequence converges to 0.
Case 3:
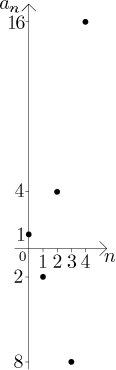
In this case the sequence does not have a limit. Note that here the divergence combines both factors that we discussed in introduction to limits: oscillation and "blowing up".
The facts about geometric sequence can be summed up in several ways. From the point of view of convergence (and not covering all alternatives) one has a nice and handy statement:
Fact.
The geometric sequence{qn} is divergent if|q| > 1 and converges to 0 if|q| < 1.
It is also possible to express all the details:
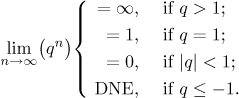
Although
Case 1: (power in the numerator). The sequence
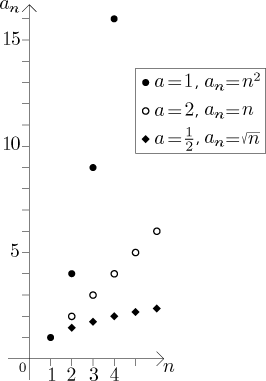
We have the following fact:
![]()
Case 2: (power in the denominator). The sequence
![]() , where
, where
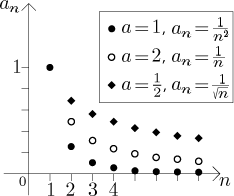
We have the following fact:
![]()
Since
This sequence is increasing, since
The limit follows by one-sided comparison, see the section Limit and comparison:
Consider the sequence
![]() .
.
![]()
Some people actually define the Euler number this way. They would say that
the Euler number
The sequences
![]()
The sequences are created by substituting natural numbers for x; that
is, by placing dots in these graphs at places where the x-coordinates
are positive integers. All properties now depend on how the dots, spaced
one-apart, fit with the period of sine and cosine, which is
Is there any pattern to the dots, for instance like this?
![]()
Pattern or no, could it happen that the dots hit the waves in such a way that eventually one has monotonicity?
![]()
Could it perhaps happen that the dots start "avoiding" hills and pits, so that the sequence eventually gets small?
![]()
Could the dots hit the waves in such a way that the sequence actually converges?
![]()
The answer to all these questions is negative. The dots hit the waves in ever changing ways that never repeat, and they do not start avoiding any areas of the sine/cosine waves. For instance, if you pick any part of the basic wave, then no matter how large a beginning of the sequence you ignore, in the remaining part of the sequence (both sine and cosine, they behave the same), the dots will again visit this segment, and if you cut this part of, then the sequence visits it again and so on. The following picture shows how the situation looks like:
![]()
What is the consequence? Since the dots in particular keep hitting hills and
pits, the sequences cannot be monotone. They will also keep getting
arbitrarily close to 1 and
For more insight into this click here.