Sequences and functions

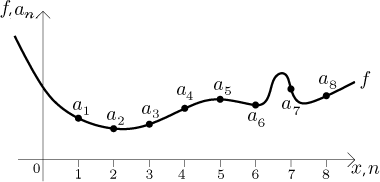
When a sequence is given by a formula (explicit definition), the same formula usually also defines a function. Indeed, there are few formulas that would work for positive integers but not for real numbers between them. One such candidate is the factorial n!, which one can extend to real numbers using the Gamma function, but it is not sufficiently popular to present a reasonable solution. Most importantly, powers with negative bases like (−1)ⁿ simply cannot be extended into functions on real numbers.

So here is the typical situation. We have a function f (x) defined on some interval (K,∞) and the same formula is used to define a sequence: a_n = f (n) for integers n > K. This means that we are picking points from the graph of f to form the sequence.

What is the connection between properties of the function and properties of the sequence?

Since the sequence is just a part of the function, it inherits the relevant properties:

Theorem.
Let f (x) be a function defined on some (K,∞), define a sequence by a_n = f (n) for integers n > K.
• If f is bounded in any sense, then also the sequence {a_n} is bounded in the same sense.
• If f is monotone, then also the sequence {a_n} is monotone (in the same direction).
• If f has a limit L as x tends to infinity, then also the sequence {a_n} has limit L.

Therefore, when investigating such a sequence, we can try to investigate the relevant function instead, using powerful tools that we have for functions, and if we get some "positive" result, it will also be true for the given sequence.

Note that this procedure only works for "positive" properties. If we learn that the function is not bounded, not monotone, or does not have a limit ("negative" facts), then we cannot carry this over to the sequence. Equivalently put, the implications in the theorem are not generally valid in the other direction. It may happen that the sequence {a_n} has all kinds of nice properties but f has none of them. The reason is simple: Since the sequence is just a small part of the whole function, knowing the behaviour of the sequence gives us no information about what happens to the function between the points of the sequence.

As an example, consider the function f (x) = x⋅sin(πx) and the sequence a_n = n⋅sin(πn).

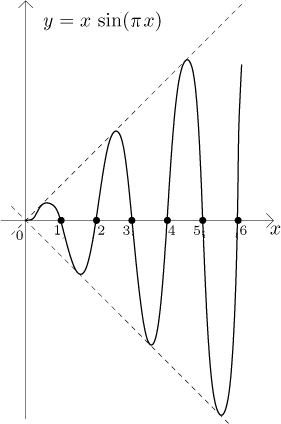
We see that the sequence actually goes {0, 0, 0, 0,...}, that is, it is a constant sequence. As a such it is monotone (both non-increasing and non-decreasing), bounded and convergent (it converges to 0). On the other hand, the function f is not bounded in any sense, not monotone and has no limit at infinity.

What does it means for our investigation of sequences? When (if) we try to investigate the relevant function instead, and get some "positive" result, it also applies to the given sequence by the above theorem. On the other hand, "negative" results (the function does not have a limit at infinity, is not increasing, etc) do not automatically apply to the given sequence. In such a situation we have to use other tools to investigate the sequence, the function approach did not help.

Example: We will show that the sequence a_n = (n − 1)/n is increasing.

Solution: We will investigate the relevant function f (x) = (x − 1)/x instead. It is defined on (0,∞), which includes all natural numbers. The derivative is f ′(x) = 1/x². Since the derivative is always positive, it follows that f is increasing on (0,∞) and therefore also the given sequence is increasing.

L'Hospital's rule
Back to Theory - Limits