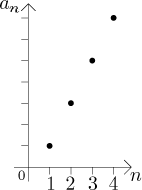
The graphs of sequences that we are using are motivated by the formal definition: that sequences are some kind od functions. Thus we start with two axes. But in fact, our intuition concerning sequences is different: We think of sequences as of a bunch of numbers going one after another. As a such, we should be able to draw them using just the real line.

As an example we look at {2n − 1}_n=1,2,3,.... We had the following graph:

But now that we are thinking of this sequence just as a bunch of numbers {1, 3, 5, 7,...}, we can try to draw them in a different way. We need just one axis, the real axis, and we will mark the numbers on this axis and indicate the order:

Similarly, the example {3, π, 2, 2, −1, 0, −1, 0, 2.5,...}, n = 0,1,2,... can be drawn like this:

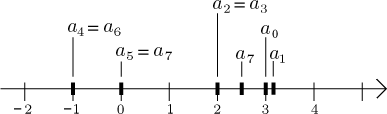
This way of drawing is in many cases more suitable, especially when it comes to interplay between sequences and functions. However, it has one drawback. If the terms of a sequence are very close, the picture becomes too crowded to show anything useful.

A bit of thinking should convince you that one can easily tell the basic properties from this new kind of picture. Bounded sequences have to stay between some bounds:

Unbounded sequences run away, for instance this one is not bounded from below (which now looks like "from the left", from the negative direction):

Increasing sequences must go from left to right, decreasing sequences must go from right to left. Oscillating sequences would jump left and right.

How about the limit? If a_n converges to L, then naturally the marks for the individual terms must get close to the mark for L.

The definition and the game can be also represented well. The tolerance ε is simply marked around L and in order to win, there must be an index (cutoff point) N so that a_N and all successive terms must stay within the given tolerance.

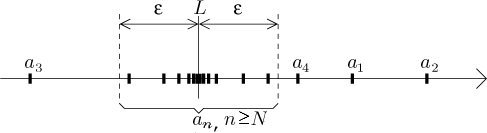
In fact, this picture suggests an alternative way to express the epsilon definition we had before:

Definition
Consider a sequence {a_n}. We say that a real number L is a limit of this sequence as n tends to infinity if for every ε > 0, only a finite number of terms a_n stays outside the range (L + ε,L − ε).