Why can't we substitute for just a part of the expression?

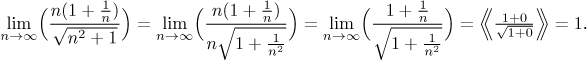
Consider the following problem. Using the "standard" way we would calculate

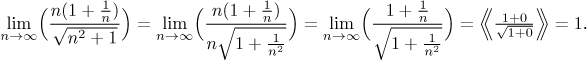
However, the second term in the numerator does not require any work, we know right away how to calculate. Why can't we just substitute infinity into it and work out the rest?

Here it perhaps does not look like a big improvement, but in some cases a trick like this can save quite a bit of work; what is more interesting, the second solution obviously leads to the same answer. The problem is that we were just lucky. Consider this problem.

We know that

(See Exercises - Simple limits.)

However, if we try to substitute infinity inside the base of the power, we get a different answer:

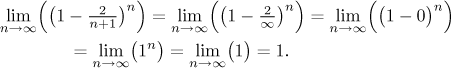
This shows that substituting just somewhere is not reliable. Perhaps you feel that the problem may have been somewhere else. In particular, if 1^∞ is an indeterminate expression, how come we wrote 1ⁿ = 1? In fact this was perfectly all right. Infinities come into play only when we try to find the outcome of a limit, then we apply the limit algebra; what happens inside a limit, before evaluating, is pure "ordinary" algebra. There are no infinitites, just the number 1 raised to some other number n, and the outcome is therefore legitimately 1.

Fine, so if what we did here was wrong, is there any way to recognize whether some "partial substitution" of infinity would work? Yes. We can substitute into just a part of the formula in cases where we are able to separate it from the rest algebraically and make it into a separate limit by using the theorem about limit and operations, then work out all limits that appear in this way and when we put their answers together, they make sense. This "making sense" part here is crucial, it decides whether separate evaluation succeeds. In the first example the separation is successful:

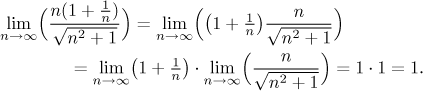
In the second example this does not work.

So this separation does not give an answer and there is no other way to somehow algebraically separate the term 2/(n + 1) from the rest; therefore it is not possible to evaluate the fraction separately from the rest of the given sequence.

In fact, if the given sequence consists of a "nice" part and a complicated part requiring further attention, then here in Math Tutor we actually recommended taking the nice part away and evaluate separately; it just has to be done properly by making separate limits and then putting their outcomes together.

Remark: Sometimes we do not need to wait for the outcomes of all limitis to see whether a separation succeeds. We know that the success depends on whether the expression we get at the end is defined. This we can often tell after evaluating just one part. For instance, in the first problem we have a product of two limits and the first one gives a one. Since there is no indeterminate product featuring 1, we know that no matter what we get for the second limit, we can always put the outcomes together and get the final answer. Therefore we can calculate the first limit right away and not copy it any more, just work on the second one. In other words, partial substitution can cause troubles only in cases where one could ran into indetermiante expressions.

Let's try another example. Since for n > 1 we have n² > n, we also have 1/n > 1/n² and therefore

However, if we try first to substitute just into 1/n, we obtain a different answer.

Indeed, here the proper calculation with decomposition into "smaller limits" would fail:

You may feel that this example was a bit artificial, that you would never think of doing anything like this. Here is another one, perhaps more reasonable.

However, we know that the fraction 1/n in the first root goes to zero, so it seemingly plays no role. If we try to just ignore it (that is, put infinity into this fraction and obtain zero), it will lead to the same answer.

Indeed, we can try to separate 1/n into an independent limit and the procedure will work out:

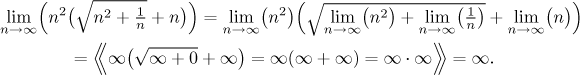
But just a little change in the problem will make this "partial substitution" procedure wrong:

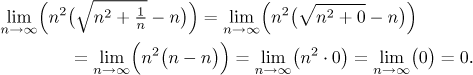
This answer is not correct, as the proper solution shows:

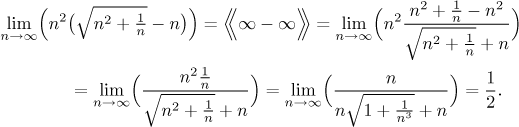
Again, if we tried to break this expression into lots of small limits, the outcomes would not combine together into a definite answer, a sure sign that "partial substitution" of infinity is out.

Great, so what is the moral of the story? That substituting infinity into just a part of the formula is not something that would work in general, so you should not do it. What does work is that you move this part into an independent limit, work out all limits that appear in this process, then put the answers together and if it makes sense, you've got your result. If you write it this way, nobody can say it's wrong.

As we saw, the only trouble is with indeterminate expressions. Indeed, the outcome of an indeterminate expression is a very delicate thing depending on a fine balance of all terms involved, so changing something there could prove fatal. As we observed, sometimes you can tell right from the start that separation will succeed, in case when the result of a separate limit cannot lead to an indeterminate expression. This is very useful and we use it quite often.