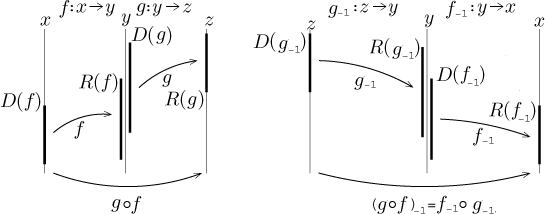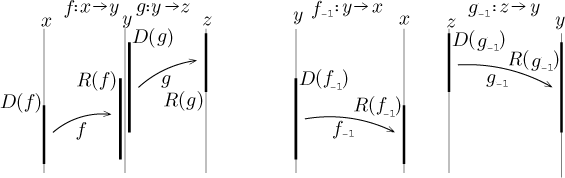Operace s reálnými funkcemi
V této sekci se podíváme na různé způsoby kombinování funkcí dohromady.
Začneme algebraickými operacemi, pak se podíváme na
skládání a nakonec krátce probereme
transformace funkcí. Sekci uzavřeme
užitečným značením pro
porovnávání funkcí.
Uvažujme dvě funkce, f a g. Abychom s nimi mohli dělat
algebraické operace (sčítání, násobení ,...), musíme nejprve ověřit, že mají
stejný definiční obor. Co se stane, když nemají? Pak jsou dvě možnosti. Jedna
je, že jejich definiční obory jsou disjunktní, v tom případě je nemůžeme
algebraicky spojovat, protože tyto dvě funkce "žijí" na zcela rozdílných
místech. V opačném případě se podíváme, kde se definiční obory protínají, a
výsledek operace bude mít tento průnik jako svůj definiční obor.
Definice (algebraické operace).
Nechť f,g jsou funkce jejichž definiční obory
nejsou disjunktní. Pak definujeme jejich
součet
f + g
vztahem
( f + g)(x) = f (x) + g(x)
pro x∈D( f ) ∩ D(g),
rozdíl
f − g
vztahem
( f − g)(x) = f (x) − g(x)
pro x∈D( f ) ∩ D(g),
násobení
f⋅g
vztahem
( f⋅g)(x) = f (x)⋅g(x)
pro x∈D( f ) ∩ D(g),
dělení f /g
vztahem
( f /g)(x) = f (x)/g(x)
pro x∈D( f ) ∩ D(g)
pro které g(x) není nula.
Jako výsledek těchto operací vždy dostaneme novou funkci, definovanou - jak
už jsme viděli - na průniku (u dělení někdy ještě na menší množině).
Vlastnosti takové nové funkce jsou obvykle jakousi kombinací vlastností
původních dvou funkcí, ale způsob jejich kombinování závisí na příslušné
vlastnosti a na operaci, takže raději tuto diskusi necháme na části, kde se
různé vlastnosti probírají. Měli bychom se zmínit o jedné, protože tato
vlastnost již byla probrána: prostota se těmito operacemi nezachovává. Pokud
začneme s dvěma prostými funkcemi a provedeme některou z těchto operací,
můžeme dostat funkci, která není prostá.
Představme si například, že máme dvě prosté funkce f a g,
jejichž hodnoty jsou mimo jiné
f (1) = 1,
f (2) = −1,
g(1) = −1, a
g(2) = 1. Kolik je
f + g v bodech 1 a 2?
Podíváme se:
( f + g)(1) = f (1) + g(1) = 1 − 1 = 0,
( f + g)(2) = f (1) + g(2) = −1 + 1 = 0.
To ukazuje, že funkce f + g
není prostá. Podobný výpočet ukazuje,
že také funkce f⋅g a
f /g nejsou prosté,
malá modifikace tohoto příkladu pak ukáže, že ani rozdíl dvou prostých funkcí
nemusí být prostý.
Protože prostota se nezachovává, nedá se také říct nic pěkného o inverzi k
výsledkům těchto operací. Neexistují žádná pěkná pravidla typu
( f + g)−1 = f−1 + g−1,
co se týče inverze, musí být výsledky těchto opeací zkoumány jako samostatné
funkce, znalost f a g nepomáhá.
Jakmile máme násobení funkcí, můžeme hned definovat obvyklým způsobem i
celočíselné mocniny funkcí, například
f 3 = f⋅f⋅f
a
f −2 = 1/( f⋅f ).
Tuto definici lze pomocí odmocnin rozšířit na racionální exponenty a pomocí
limitního přechodu definovat f a
pro libovolné reálné a. Pro detaily viz
Mocniny v části Teorie -
Elementární funkce.
Posledním krokem je definice obecné mocniny
f g pomocí
( f g)(x) = e g(x)⋅ln( f (x))
pro
x∈D( f ) ∩ D(g)
pro která f (x) > 0.
Pro detaily se podívejte na
Obecné mocniny v části Teorie -
Elementární funkce.
Skládání (kompozice)
Pro následující operaci je výhodné si připomenout alternativní vizualizaci
funkce. To, že f posílá body z jedné množiny (podmnožiny reálných
čísel) na body z jiné množiny, se dá vyjádřit takto:
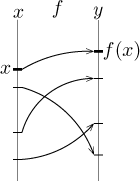
Hodnoty funkce f jsou zase čísla, takže je lze použít jako argumenty
další funkce g takto:
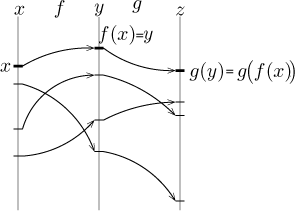
Jako celek vznikne procedura, která posílá čísla z jedné kopie reálných čísel
(značených pomocí x) do další kopie označené pomocí z, můžeme
zapomenout, že tam byl nějaký prostřední krok a prostě považovat celou věc za
nějakou funkci.
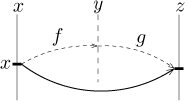
Tato nová funkce se nazývá skládání či kompozice daných dvou
funkcí a aby tento nápad fungoval, je třeba jedné podmínky: Aby hodnoty
f ležely v definičním oboru g (všechny nebo alespoň některé).
Jak se tohle zapisuje? Jedno značení je přirozené. Začneme s x, pak
aplikujeme f a dostaneme číslo
y = f (x).
Na toto číslo aplikujeme g, čímž obdržíme
z = g( y) = g( f (x)).
Takže g( f (x)) je značení pro skloženou funkci
aplikovanou na číslo x; všimněte si, že když máme takovou kompozici,
pak ji počítáme zevnitř ven, tj. začneme s x a propracujeme se
ven vykonáním potřebných operací. To ostatně není překvapivé, když máte
spočítat (3 + 2)2, začnete sečtením 2 a 3,
nikoliv umocňováním (protože dokud nesečtete, nevíte co umocnit). Přirozeně se tak f
nazývá vnitřní funkce a g se říká vnější funkce.
Protože x ↦ g( f (x))
dává předpis pro posílání čísel
x někam, vzniká vlastně nová funkce a ta si zasluhuje vlastní značení.
Jedno možné je g( f ). Všimněte si, že když počítáme takto
značenou funkci, pak nejprve aplikujeme vnitřní funkci, takže například číslo
2 se dosadí takto:
g( f )(2) = g( f (2)).
Jinými slovy,
g( f ): x ↦ g( f (x)).
Toto je jedno značení pro kompozici, ale matematici dávají přednost značení
jiného typu, protože ti rádi vyjadřují operaci nějakým symbolem mezi dvěma
zúčastněnými funkcemi. Proto také používáme toto značení:
g ○ f. Všimněte si, že toto se čte zprava doleva! Nejprve
se aplikuje funkce napravo a pak funkce nalevo. Proč? Protože to pak ladí s
předchozím značením. Dostaneme
(g ○ f )(x) = g( f (x)),
pořadí tedy zůstává stejné. Skvělé, deset bodů za logiku, ale stejně je to
matoucí pro spoustu začátečníků. Dejte si pozor.
Příklad.
Uvažujme funkce
f (x) = x + 2 a
g(x) = x2. Kolik je
(g ○ f )(1)?
(g ○ f )(1) = g( f (1)) = g(1 + 2) = g(3) = 32 = 9.
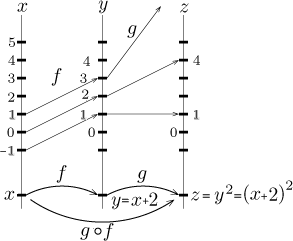
Jak to funguje? Číslo x = 1 se dosadí do f a dostane
se y = f (1) = 3. Protože g působí na
hodnoty f značené pomocí y, možná je teď dobré si přepsat
g jako
g( y) = y2. Dosazením
za y teď dostaneme
z = g(3) = 9.
Snadno se ověří, že (g ○ f )(x) = (x + 2)2
pro libovolné x. Všimněte si, že jsme použili funkce, které mají jako
definiční obor celou reálnou osu, abychom se vyhnuli problémům s tím, jaké
argumenty jsou povoleny.
Protože nemáme potíže s definičními obory, můžeme také zkusit prohodit
pořadí, ve kterém tyto funkce skládáme. Protože jména proměnných jsou jen pro
naše pohodlí, nemělo by nás trápit, že f "očekává" x, ale
výsledky g byly zvané z. Máme prostě novou situaci, takže
můžeme použít jiná písmena pro proměnné, abychom to vystihli. To je vlastně
pro matematiku typické, jsou nicméně situace, kdy proměnné mají specifický
význam a pak je lepší ponechat dané proměnné (například když se pracuje s
inverzními funkcemi, v aplikacích atd).
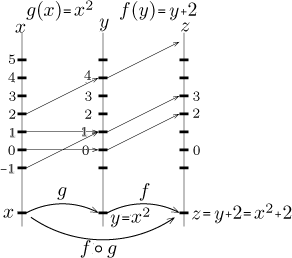
Jak vidíte,
( f ○ g)(x) = f (x2) = x2 + 2.
Toto ukazuje, že skládání funkcí rozhodně není komutativní, tj.
f ○ g
nemusí být stejné jako g ○ f
(a v typickém
případě také není).
Teď víme, jak to funguje, takže pro úplnost přidáme také formální definici.
Definice.
Nechť f a g jsou funkce takové, že
R( f ) není disjunktní s
D(g).
Pak definujeme kompozici f a g jako
funkci definovanou pro x z množiny
D(g ○ f ) = {x∈D( f ); f (x)∈D(g)}
vzorcem
(g ○ f )(x) = g( f (x)).
Samozřejmě, máme-li více funkcí, mohou se skládat v řetězec, pokud tedy
pasují jejich definiční obory a obory hodnot:
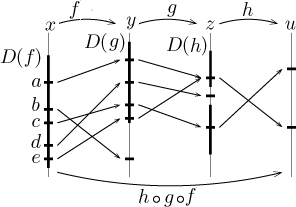
Označili jsme definiční obory zúčastněných funkcí. Z vyznačených hodnot
x patří pouze a, c a e do definičního oboru
složené funkce
h ○ g ○ f.
Vidíme, že číslo b je pomocí f posláno
na určité číslo f (b), které není v definičním oboru funkce
g, takže na něj tuto funkci nelze aplikovat. Číslo d bylo
nejprve v pohodě, protože f (d) patří do
D(g);
proto d patří do definičního oboru složené funkce
g ○ f.
Nicméně když
se aplikuje g na f (d), obdržená hodnota již neleží v
definičním oboru h a proto poslední krok v kompozici selže.
Abychom ukázali, jak je pasování definičních oborů podstatné, podíváme se na
tento příklad:
Příklad.
Uvažujme
f (x) = −1 − x2
a g(x) = x1/2 (g je
odmocnina). Vidíme, že definiční obor f je celá reálná osa (s
umocňováním není problém), její obor hodnot je interval
(−∞,−1⟩.
Definiční obor g je
⟨0,∞), protože nejde odmocňovat
záporná čísla. Protože obor hodnot f neprotýká definiční obor
g, nemůžeme je skládat v pořadí
"nejprve f, pak g", tj.
g ○ f. Ověřte si, že
ať už zkusíte jakékoliv číslo x, dosazením do
(g ○ f )(x ) = (−1 − x2)1/2
se dostaneme do průšvihu. Například
(g ○ f )(2)
by měla být odmocnina z −5, což neexistuje (ve světě reálných čísel).
Můžeme ale bez problémů skládat opačným způsobem, protože obor hodnot
g (nezáporná čísla) je podmnožinou definičního oboru f. Můžeme
počítat
( f ○ g)(x) = f (x1/2) = −1 − (x1/2)2.
Tato nová funkce má díky odmocnině definiční obor
⟨0,∞).
Algebraicky lze tento vzorec zjednodušit na
−1 − x, ale je
třeba mít na paměti, že coby výsledek skládání se pouze uvažuje na intervalu
⟨0,∞).
Kdybychom dostali tento
vzorec jako nezávislou funkci, neovlivněnou nějakou historií, určili bychom
definiční obor −1 − x coby celou reálnou osu.
Skládání se chová pěkně vzhledem k prostotě. Jestliže jsou f a
g obě prosté, pak jejich složení (v libovolném pořadí, které dává
smysl) je také prosté (formálně to budeme formulovat níže). Pokud není jedna
či obě funkce prosté, pak se o jejich složení nedá nic říct.
Připomeňme, že prostota je blízce svázána s existencí inverzní funkce. Když
teď máme zavedeno skládání, můžeme přepsat definici inverzní funkce. Je-li
dána prostá funkce f, její inverzní funkce f−1 je
charakterizována těmito rovnostmi:
•
f−1( f (x)) = x
pro všechna x z D( f ),
•
f ( f−1( y)) = y
pro všechna y z R( f ).
V jazyce skládání je inverzní funkce určitá funkce, která splňuje
f−1 ○ f = ID( f )
a f ○ f−1 = IR( f ),
kde IM je identita na množině M, pro další
informace viz
Identita v části
Teorie - Elementární funkce.
Věta (skládání a inverze).
Nechť f a g jsou prosté funkce, pro které
má smysl skládání g ○ f. Pak je
funkce g ○ f také prostá a pro její inverzní funkci
platí
(g ○ f )−1 = f−1 ○ g−1.
Všimněte si, že inverze převrací pořadí skládání, to je důležité, protože
víme, že skládání rozhodně není komutativní. To o "skládání má smysl"
znamená, že obor hodnot f protíná definiční obor g, takže
jejich kompozice je definována pro alespoň jednu hodnotu x. Protože
definiční obor a obor hodnot inverzní funkce jsou obor hodnot a definiční
obor původní funkce, také skládání inverzí má smysl, tj. obor hodnot
g−1 bude protínat definiční obor f−1.
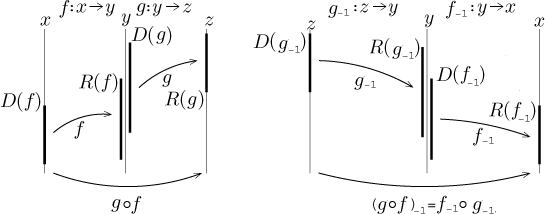
Pokud bychom zkusili složit inverze opačně, pak už to nemusí platit.
Mimochodem, tohle je zrovna případ, kdy se vyplatí zachovávat jména
proměnných. Původní skládaná funkce posílá x na z. Inverze by
proto měla posílat z na x. To platí, pokud skládáme tím
správným zůsobem popsaným výše, ale nefunguje to, když to zkusíme naopak.
Teď se dokonce ani neshodují proměnné, netvoří řetězec, což by mělo naznačit,
že je tu něco špatně.
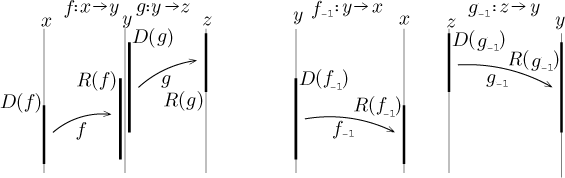
Transformace
Operace s funkcemi mají jeden speciální případ, a to když jedna z nich je
konstantní funkce. Ta druhá funkce je pak transformována. Uvažujme tedy
funkci f (x) a reálné číslo c.
Případ 1:
Definujme
g(x) = f (x) + c,
neboli krátce
g = f + c. Funkce g má všechny své
hodnoty posunuty o stejně mnoho, takže její tvar zůstane stejný. Graf
g se získá posunutím grafu f
nahoru o c, jestliže c je kladné, nebo dolů o
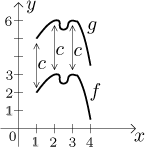
|c|, je-li c záporné. Na následujícím obrázku máme
g = f + 3, proto se graf g získá posunutím grafu
f nahoru o 3.
Případ 2:
Definujme
g(x) = f (x + c).
Funkce
g má svůj argument zvýšen vždy o stejně mnoho. Pokud si pod x
představíme čas a na chvíli si vezmeme c kladné, pak g v čase
x se obdrží tak, že se podíváme na f v čase o něco do
budoucnosti, což znamená doprava na ose x. Jinými slovy, hodnotu
g dostaneme tak, že se díváme na graf f o něco doprava; graf
g bude proto úplně jako graf f, ale posunut doleva. Podobně se
pro c záporná díváme na f v dřívějším čase. Obecně pro Případ 2
tedy řekneme, že tvar zůstává, graf g se dostane posunem grafu
f doleva o c pro c kladné nebo doprava o
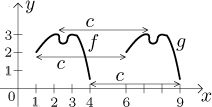
|c| pro c záporné. Na následujícím obrázku ukážeme graf
g(x) = f (x − 5),
bude to tedy graf f posunutý doprava o 5.
Případ 3:
Definujme
g(x) = c⋅f (x),
neboli krátce g = c⋅f. Funkce
g má všechny své hodnoty násobeny stejným číslem. Jestliže
c > 1, pak v místech, kde je g velká, se o mnoho zvětší,
zatímco tam, kde je g malá, se zvětší, ale jen o trochu. Například pro
c = 2 je dvakrát velké číslo docela velká změna, zatímco
dvakrát skoro nula je pořád více méně nula. Na následujícím obrázku máme
g(4) = 2⋅f (4) = 2⋅0 = 0,
což neznamená žádnou změnu, zatímco
g(2) = 2⋅f (2) = 2⋅3 = 6,
což je velká změna.
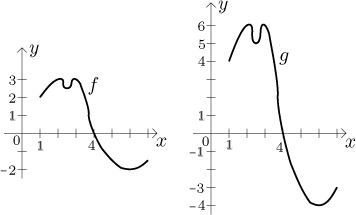
Slovy, čím větší jsou hodnoty f - tj. čím dále je graf f od osy
x - tím větší je změna při přechodu k
g = 2⋅f. Z toho se odhadne, že graf g
se získá proporcionálním protažením vzhledem k ose x (tj.
změnou velikosti amplitudy). Jestliže
c > 1, hodnoty se zvětší a graf
se natáhne, jestliže
0 < c < 1, hodnoty
se zmenší a graf se zcvrkne.
Jestliže je c záporné, pak zase máme tu roztahovací/zcvrkávací
alternativu podle toho, jak se |c| porovná s 1, ale tentokráte se také
graf překlopí okolo osy x. U tohoto případu tedy jde o změnu
měřítka pro hodnoty funkce. V následujícím obrázku si nejprve připomeneme
funkci f použitou výše, pak ukážeme graf
g = 2⋅f a graf
g = −1/2⋅f.
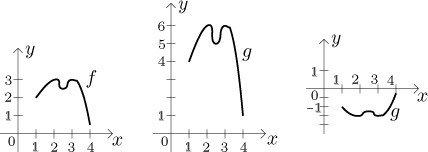
Speciální případ:˙g = −f má graf stejný jako graf
f, ale překlopen symetricky kolem osy x.
Případ 4:
Definujme
g(x) = f (c⋅x).
Abychom viděli efekt této transformace, představíme si, že jedeme po cestě a
f je výška kopců podél cesty. Co to znamená, když teď uvažujeme
g(x) = f (3⋅x)? K získání
g v čase x se podíváme na f v čase třikrát větším. Tato
transformace tedy odpovídá urychlení času, a když jedeme rychleji, zdá se, že
kopce přicházejí rychleji, jako by byly blíže. Proto graf této g bude
stejný jako graf f, ale stlačen třikrát ve vodorovném směru. Podobně
jako v předchozím případě, čím dále jsme od osy y, tím větší změna.
Jestliže 0 < c < 1,
pak se čas zpomalí a graf se natáhne, aby šel
pomaleji. Na následujícím obrázku ukážeme
g(x) = f (x/2).
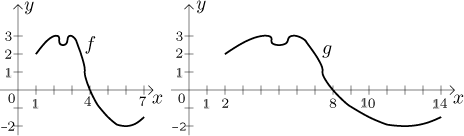
Například
g(10) = f (10/2) = f (5) = −3/2.
Mělo by to znít rozumně, předtím nám to trvalo 4 hodiny, než jsme se dostali
skrz ten dvouhrbý kopec, s funkcí g to trvá dvakrát tak dlouho.
Obecně se tedy graf funkce g dostane v případě
c > 1
protažením grafu f c-krát ve vodorovném směru, vzhledem
k ose y, a v případě
0 < c < 1
zmáčknutím grafu f
1/c-krát ve vodorovném směru, vzhledem k ose y. Jestliže je
c záporné, graf se zase transformuje ve vodorovném směru podle toho,
jak se |c| porovná s 1, ale teď je také třeba překlopit graf podle osy
y. V tomto případě jde o změnu měřítka pro argument.
Na následujícím obrázku si nejprve připomeneme již dříve použitou
f, pak ukážeme grafy
g = f (2⋅x)
a g = f ((−1/2)⋅x) (porovnejte to s
posledním příkladem).
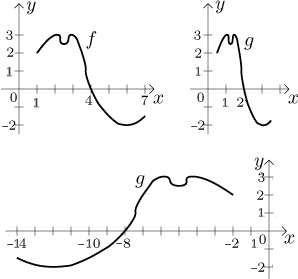
Speciální případ:
g(x) = f (−x) má graf
jako je graf f, ale překlopený symetricky okolo osy y.
Můžeme odhadovat grafy i docela složitých funkcí, pokud známe grafy
elementárních funkcí a aplikujeme na ně transformace. Viz
Transformace a odhad grafu
v Přehledu metod.
Obecně je prakticky nemožné odhadnout graf funkce vzniklé ze dvou pomocí
algebraických operací. Občas máme štěstí, nejsnadnější případ je
f + g.
V každém x se přičte hodnota
g k hodnotě f (dá se jakoby nad ní). Můžeme si představit
hodnoty g jako tyčky příslušné výšky, které posuneme nahoru a dolů
tak, aby jejich základny přesně pasovaly nad graf f.
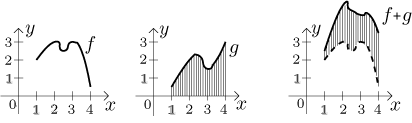
Tohle ale vyžaduje spoustu zkušeností a představivosti, a tak se to moc
nepoužívá.
Krátký zápis, porovnávání
Už jsme viděli příklad krátkého zápisu,
g = f + c znamenalo
g(x) = f (x) + c
pro všechna x. Obecně, když napíšeme rovnost či nerovnost s funkcemi, ale bez
zápisu proměnných, tak se automaticky předpokládá, že tato rovnost/nerovnost
platí pro všechny možné hodnoty argumentu. Tedy
h = f + g znamená
h(x) = f (x) + g(x)
pro všechna x z průniku definičních oborů funkcí f a g.
Podobně f ≤ g znamená
f (x) ≤ g(x)
pro všechna x z průniku
definičních oborů f a g. Takto porovnáváme funkce. Je pět
možností. Můžeme mít f ≤ g, jak jsme to právě
viděli, nebo f < g, což znamená
f (x) < g(x) pro všechna x z průniku
definičních oborů; v opačném směru jsou možné nerovnosti
f ≥ g
nebo
f > g; no a může se také stát, že žádné porovnání není
možné, jinými slovy že pro některá x je větší funkce f, pro
jiná x je zase větší funkce g.
Základní vlastnosti reálných funkcí
Zpět na Teorie - Reálné
funkce