Transformace a odhad grafu: Přehled metod

Zde se pokusíme objasnit, jak odhadnout graf funkce, která byla získána aplikováním transformací na známou funkci. Nepokryjeme tak funkce, které jsou získány kombinováním více funkcí, protože pak je odhad grafu obtížný, často nemožný. Situace, kterou zde pokryjeme, je následující. Máme jednu elementární funkci a aplikujeme na ni jednu či více transformací. Pokud jste se již podívali na poznámku o pořadí výpočtu a algebraickém znázornění funkce, tak rozumíte, když řekneme, že zde nebudeme hádat grafy funkcí, které nejsou jeden řetězec, ale mají více "kořenů". Mimochodem, to pořadí výpočtu se tu také může hodit.

Důležitou součástí této sekce je seznam transformací a jejich vlivu. Protože nás tu zajímá praxe, uděláme "špatný" seznam ve smyslu, že jedna transformace bude pokryta několikrát, rozdělena na speciální případy. Například změna měřítka cx bude rozdělena do čtyř částí, protože když řešíme problém, tak je to pro nás intuitivně jednodušší. Více detailů o transformacích lze najít v sekci Operace, my zde jenom symbolicky znázorníme jejich efekt. Na konci sekce se také zmíníme o tom, jak odhadnout efekt funkcí, které nepatří mezi tradiční transformace, ale zkušenému studentovi by ta poznámka mohla občas pomoci.

Každá transformace funguje stejným způsobem, nahrazováním. Každá transformace také přichází ve dvou verzích, lze ji aplikovat na argument nebo na hodnotu (tj. na funkci). Když například násobíme číslem c, můžeme buď nahradit všechna x ve vzorci výrazem c⋅x (změna argumentu), nebo můžeme vzít vzorec, který zrovna máme, a vynásobit jej c, tj. nahrazujeme určitý vzorec f (x) vzorcem c⋅f (x). Tuto nahrazovací proceduru budeme representovat šipkou.

Algoritmus pro odhad
Krok 1. Určete základní elementární funkci, jejíž graf je základem pro danou funkci.
Krok 2. Načrtněte graf základní funkce, pak jej upravte podle transformací, které byly aplikovány na argument (od poslední k první vzhledem k pořadí operací, viz níže).
Krok 3. Vezměte graf z kroku 2 a upravte jej podle transformací, které jsou aplikovány na hodnotu (od první k poslední vzhledem k pořadí operací, viz níže).

Jedna z nějtěžších věcí pro studenty je rozpoznat správné pořadí, v jakém aplikovat transformace. V typickém případě jsou na argument aplikovány dvě transformace, otázka pak je, kterou začít. Naštěstí existuje snadný způsob, jak na to přijít. Když začnete s x a aplikujete nahrazování, jak je ukázáno těmi šipkami výše, měli byste dostat argument dané funkce. Pokud dostanete něco jiného, vaše pořadí bylo chybné. Toto pravidlo také funguje, když je aplikováno více transformací.

Když například hádáme graf funkce sin(2x + 3), je tu otázka, zda máme nejdřív posunout graf doleva o 3 a pak jej dvakrát zmáčknout, nebo jej nejprve dvakrát zmáčknout a pak teprve posunout o 3 doleva. Zkusíme si teď pro obě varianty ten nahrazovací postup:
Nejprve posun, pak zmáčknutí odpovídá pořadí nahrazení
        x → (x − 3) → (2x − 3),
v druhém kroku nahrazujeme x výrazem 2x.
Nejprve zmáčknutí, pak posun odpovídá pořadí nahrazení
        x → 2x → 2(x − 3),
v druhém kroku nahrazujeme x výrazem (x − 3), takže závorky byly nutné.

Vidíme, že pro transformaci 2x − 3 je správné první pořadí. Existuje delší ale možná výmluvnější způsob zápisu, jak transformace (tj. nahrazování) ovlivní počáteční funkci. Ukážeme to pro tu první (správnou) variantu.

 T   f (x)
    x
x ↦ x − 3:   x − 3
x ↦ 2x: (2x) − 3

Poznámka: Pokud se podíváme na pořadí, ve kterém daný výraz počítáme, pak by měly být transformace aplikovány "od poslední k první". Kdybychom chtěli počítat výraz 2x − 3 na kalkulačce pro určité konkrétní x, nejprve bychom násobili a pak odčítali, což souhlasí, jak jsme viděli, transformace by měly jít v opačném pořadí. Od poslední k první je pravidlo, které si můžete zapamatovat, ale jen pro argument. Transformace, které se aplikují na hodnotu, se dělají přesně naopak, od první k poslední.

Příklad: Odhadněte graf funkce

Řešení: Nejprve určíme základní funkci. Protože nám transformace nedovolují dělit, začneme se zlomkem 1/x. Vidíme druhou mocninu, která taky nejde udělat transformacemi, takže se zdá, že základní funkce je 1/x2. A je tomu tak, všechny další operace, které se objevují v f, jsou transformace.

Teď máme aplikovat transformace, které mění argument x, potřebujeme jej změnit v (3x − 2), což je výraz uvnitř druhé mocniny. Znamená to zmáčknout graf třikrát ve vodorovném směru (směrem k počátku) a posunout jej doprava o 2. Co přijde dřív? Pokud nejprve dilatujeme a pak posuneme, nahrazování udělá

x → 3x → 3(x − 2).

To nesedí, musíme to tedy udělat naopak, nejprve posun, pak dilatace.

x → x − 2 → 3x − 2.

Nemělo by to překvapit, "− 2" se dělá poslední (po "3 krát"), takže dle pravidla tím máme začít (posunem). Uděláme tedy toto:

Existuje jakási kontrola, zda jsme to udělali správně. Funkce 1/(3x − 2)2 má problém (díru v definičním oboru) v bodě 2/3, což zdá se souhlasí s naším obrázkem, takže je snad dobře. Kdybychom ty dvě transformace použili ve špatném pořadí, dostali bychom něco jiného:

Mimo jiné vidíme, že díra v definičním oboru teď nesouhlasí.

Teď je tedy čas aplikovat transformace na hodnotu. Jsou tři, svislé zvětšení čtyřikrát, posun dolů o 1 a zrcadlení pomocí absolutní hodnoty. Absolutní hodnota se počítá nakonec, takže bude také poslední aplikovaná. Pravidlo "od prvního k poslednímu" říká, že bychom nejprve měli udělat svislou dilataci 4 krát, pak posun dolů o 1 a nakonec to zrcadlení. Pro jistotu se podívámě, že to nahrazování sedí:

Nakonec jsme dostali správný výraz, takže to udělejme. Nejprve dilatace a posun,

nakonec zrcadlení.

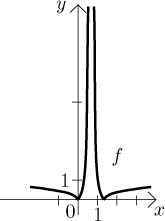
Docela pomůže, když během kroků hlídáme pozice některých významných bodů, například zkusíme dosadit nulu nebo kontrolujeme nulové body. Zde je na závěr ověříme, že nulové body dané funkce jsou x = 0 a x = 4/3, což obrázek zachytil dobře.

Pár dalších transformací

Zde probereme tři další transformace. Jsou docela pokročilé a ve většině kursů kalkulu se ani neprobírají. My je tu dáváme, protože jsou občas užitečné (už mi párkrát pomohly) a tato sekce by se bez nich necítila úplná.

Umocňování. Zde je situace: Známe graf nějaké funkce f. Jak vypadá graf funkce f 2?

Druhá mocnina kombinuje dva efekty. Ten první je, že mění všechny záporné hodnoty na kladné, takže bychom měli začít zrcadlením záporných částí grafu f nad osu x. Druhý efekt je, že se změní velikosti ve svislém směru, ale na rozdíl od dilatací probraných výše nejde o roztahování stejným faktorem. Stručně, čím větší je hodnota f, o to více se zvětší umocněním. Například tam, kde je f rovno 10, se graf natáhne ve svislém grafu 10 krát, v místech, kde je f rovno 1, s ním neudělá umocnění nic a v místech, kde f je 1/2, dokonce umocnění vydělí výšku grafu na polovinu! To naznačuje, jaké kroky dělat:

1. Nejprve zrcadlíme graf jako při kreslení | f |. Pak děláme následující.
2. Body, kde | f | = 1 a kde f = 0, zůstanou, kde jsou.
3. Body, kde | f | > 1, budou poslány dále od osy x, tj. graf se tam roztáhne ve svislém směru; čím dále je | f | od osy x, tím více se tam graf natáhne.
4. Body, kde | f | < 1, budou poslány blíže k ose x, tj. graf tam bude smrsknut k ose x; čím blíže je | f | k ose x, tím více bude graf zmáčknut.

Pokud se to udělá správně, pak monotonie f 2 musí být přesně stejná jako monotonie | f |. Jinými slovy, na intervalech, kde | f | je rostoucí, musí být rovněž graf f 2 rostoucí, totéž platí o intervalech klesání.

Příklad: Na levé straně je graf nějaké funkce f, vyznačili jsme také účinek zrcadlení a úroveň 1. Napravo je graf f 2.

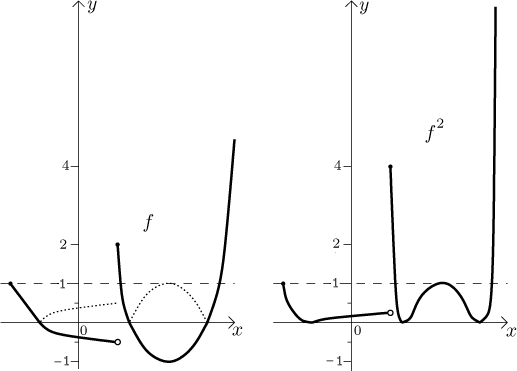
Poznámka: Efekt ostatních celočíselných mocnin větších než 1 je podobný. Sudé fungují naprosto stejně, jen ten natahovací a smrskávací efekt je větší pro mocniny větší než 2. Liché mocniny větší než 1 mají tentýž natahovací/smrskávací účinek, ale bez zrcadlení.

Odmocnina. Zde je situace: Známe graf nějaké funkce f. Jak vypadá graf druhé odmocniny z f ?

Druhou odmocninu můžeme aplikovat pouze na funkce, které nenabývají záporných hodnot. Zde si potřebujeme pamatovat, že odmocnina dělá čísla větší než 1 menšími, ale zvětšuje čísla menší než 1. To naznačuje potřebné kroky.


1. Body, kde f = 1 a kde f = 0, zůstanou, kde jsou.
2. Body, kde f  > 1, budou poslány blíže k ose x, tj. graf tam bude zmáčknut směrem k ose x; čím dále je f od osy x, tím více se graf zmáčkne.
3. Body, kde f  < 1, budou poslány dále od osy x, tj. graf se tam natáhne; čím blíže je f k ose x, tím více se graf natáhne.

Pokud se to udělá správně, pak monotonie f 1/2 musí být přesně stejná jako monotonie f. Jinými slovy, na intervalech, kde f je rostoucí, musí být rovněž graf f 1/2 rostoucí, totéž platí o intervalech klesání.

Příklad: Nalevo je graf nějaké funkce f, zaznačili jsme také úroveň 1. Napravo graf funkce f 1/2.

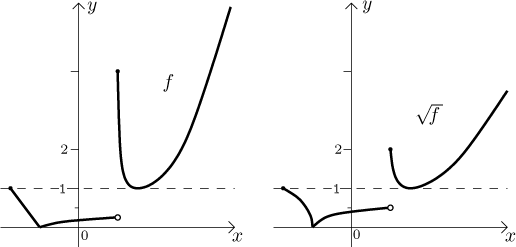
Poznámka: Efekt dalších odmocnin je podobný. Je-li n sudé přirozené číslo, pak n-tá odmocnina funguje stejně jako druhá. Jestliže je n liché, pak má n-tá odmocnina podobný efekt, ale může být aplikovaná na všechny funkce a jejich záporné části jsou změněny stejně, jako jsme transformovali kladné části.

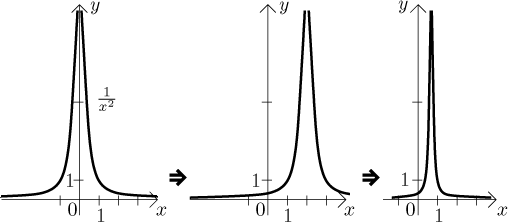
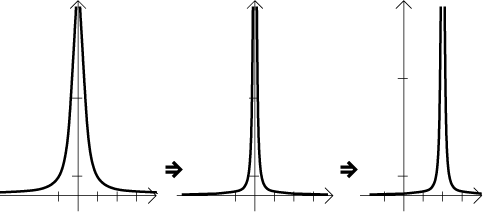
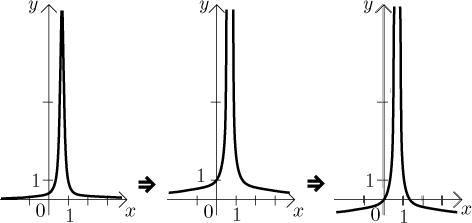
Převrácená hodnota. Zde je situace: Známe graf nějaké funkce f. Jak vypadá graf funkce 1/f ?

Převrácenou hodnotu lze aplikovat pouze na funkce, které nejsou nula. Víme, že převrací velká čísla na malá a naopak, ale znaménko se zachovává, což naznačuje, jak se to bude dělat.


1. Rozdělíme graf na vodorovné pruhy. První pruh je oblast daná nerovnicí y > 1, obsahuje tedy všechny části grafu, kde f  > 1. Druhý pruh je ten mezi úrovněmi y = 1 a y = 0. Třetí pruh je mezi úrovněmi y = 0 a y = −1. Poslední pruh je oblast pod y = −1.
2. Body, kde f = 1 a f = −1, zůstanou, kde jsou.
3. Části grafu, které jsou v prvních dvou pruzích, si vymění místa. Body, které byly blízko úrovně y = 1, zůstanou blízko. Body, které byly dále, zůstanou dále následujícím způsobem: Části grafu, které utíkaly do nekonečna, teď půjdou do 0. Části grafu, které se blížily k 0, budou poslány do nekonečna. Je to trochu jako překlápění okolo přímky y = 1, které se musí vejít do horní poloroviny.
4. Ty dva pruhy v dolní polorovině se prohodí přesně jako v 3., teď ale všechno je a zůstane záporné.

Pokud se to udělá správně, bude monotonie grafu 1/f přesně opačná k monotonii f. Přesně, na intervalech, kde je f rostoucí, musí být graf 1/f klesající a naopak.

Příklad: Nalevo graf nějaké funkce f, označili jsme také úroveň 1. Napravo graf f −1.

Poznámka: Když dáme nápady z částí 1 - 3 dohromady, umíme teď také hádat záporné mocniny a odmocniny.

Zkušený hadač grafů by se také uměl vypořádat s věcmi jako ln( f (x)) nebo e f (x), ale to už bychom opravdu zacházeli příliš daleko, tak toho necháme.

 

Pro další příklady odkazujeme na Řešené příklady.

Zpět na Přehled metod - Základní vlastnosti reálných funkcí