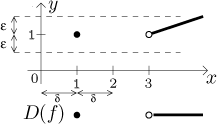
Jak se často stává, ohledně definice spojitosti jsou dvě školy. My jsme zde požadovali, aby funkce byla definována na nějakém okolí zkoumaného bodu a, protože když f okolo a neexistuje, pak se zdá zbytečné se zajímat, jestli se tam graf blíží k příslušnému bodu - graf tam kolem žádný není! Takže ta definice, kterou tu máme, vypadá rozumně a je také vhodnější pro základní kalkulus. Nicméně někteří lidé dávají přednost tomu, že tento předpoklad vynechají, klidně se ptají na spojitost i v bodech, okolo kterých funkce třeba vůbec neexistuje. Taková definice je popravdě řečeno docela odůvodněná, protože pak souhlasí s velice obecnou definicí spojitosti pro zobrazení a matematici mají rádi, když věci hrají dohromady.
Po docela těžkém rozjímání (autor sám je koneckonců matematický vědátor) jsme se rozhodli použít tu definici, co je nahoře, protože Math Tutor rozhodně není pro vědce, ale pro normální lidi, kteří se snaží přežít přednášky kalkulu. Ve většině případů tyto dvě definice dají stejné výsledky, těch pár rozdílů většinou nepůsobí problémy. Stejně si ale dejte pozor, jakou definici používá váš profák, a buďte ostražití. Abychom ukázali alespoň jeden příklad rozdílu v definicích, podívejme se na následující funkci.

Podle naší definice bychom se ptali na spojitost v a pro
Lidé, kteří dávají přednost alternativní definici, by se ale ptali také na
spojitost v