Absolutní hodnota

Definice.
Absolutní hodnota reálného čísla x, značená |x|, je definována jako

Příklad: |4| = 4, |1/13| = 1/13, |0| = 0, |−5| = 5 (což je opravdu -(−5)), |-0.137| = 0.137.

Poznámka: Když normálně definujeme funkci rozpisem, definiční obory jednotlivých případů mají být disjunktní. Zde jsme dali rovnost u obou vzorců, protože pro x = 0 vycházejí stejně. V praxi se obvykle bere jedna nerovnost s rovností a druhá ostrá, typicky ta x < 0, ale není to nutné.

Graf:

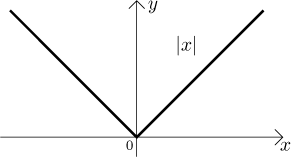
Vlastnosti jsou jasné z obrázku, funkce je spojitá, sudá, klesající na (−∞,0⟩ a rostoucí na ⟨0,∞). Co se týče derivace, nedá se zapsat vzorcem, místo toho musíme rozlišit případy:

Neexistuje derivace v nule, ale máme tam jednostranné derivace, |x|'_-(0) = −1, |x|'₊(0) = 1.

Absolutní hodnota je pro studenty velmi populární zdroj potíží, často se snaží nějak vykouzlit derivaci a dostávají úžasné výsledky. Bohužel, velmi málo se dá udělat (výpočetně) s absolutní hodnotou přímo. Ve většině případů se jí potřebujeme zbavit tak, že se situace rozdělí na případy podle znaménka výrazu uvnitř absolutní hodnoty (přesně podle definice) a pak pracovat dál. Pokud na to budete pamatovat, neměli byste mít problémy. Pro detaily a příklady viz například sekce o práci s funkcí danou rozpisem v části Derivace - Přehled metod - Průběh funkce a Průběh funkce v části Derivace - Řešené problémy.

Poznámka: Existuje alternativní způsob zápisu absolutní hodnoty: |x| = x⋅sign(x). Protože funkce sign je definována rozpisem a při práci zase musíme rozdělit situaci na případy, nic si tím neušetříme, ale může to takto vypadat více přátelsky, zejména když pak máme pěkný vzorec pro derivaci: |x|' = sign(x) pro nenulové x. Můžeme tak snadno zapisovat derivace výrazů s absolutní hodnotou, vzorce jsou roztomilé, ale může to být zrádné, protože je nutné si při používání tohoto zápisu pamatovat, že neexistuje derivace v 0. Pro více detailů viz další sekce.

Funkce sign
Zpět na Teorie - Elementární funkce