Dirichletova funkce a její modifikace

Začneme s definicí Dirichletovy funkce.

Definice.
Dirichletova funkce je definována vzorcem

Připomeňme si, že jak racionální čísla (kde d = 1), tak iracionální čísla (kde d = 0) jsou husté na reálné ose. Znamená to, že když vezmeme nějaký otevřený interval, jakkoliv malý, vždy v něm budou nějaká racionální a iracionální čísla. Intuitivně, racionální a iracionální čísla jsou všude. Proto je pak nemožné tuto funkci správně nakreslit, měli bychom nakreslit dvě vodorovné přímky, ale ne zcela přímky:

Protože racionální a iracionální body jsou všude, tyto dvě "přímky" v sobě ve skutečnosti mají díry; tyto díry jsou všude, neexistuje nikde ani ten nejmenší kousek nepřerušované čáry. Když se například podíváme na tu horní "přímku", pokaždé když vezmeme dvě racionální čísla, bude mezi nimi nějaké iracionální dělat v horní lini díru. Podobně je mezi libovolnými dvěma iracionálními čísly, jakkoliv blízkými, nějaké racionální, které pak udělá díru v dolní "přímce".

Takže díry jsou všude, ale jsou vždycky přesně velikosti jedné díry, nikdy nevytvoří větší díru, z důvodů podobných těm nahoře. Například když vezmeme dvě díry v horní "přímce", tak odpovídají dvěma iracionálním číslům, a protože je mezi nimi určitě nějaké racionální číslo, udělá v horní "přímce" tečku a tím oddělí ony dvě díry.

Jaké jsou vlastnosti této funkce? Nejprve si všimněme, že neexistuje jediný bod, kde bychom měli nějakou jednostrannou limitu. Schválně si vyberme nějaké a. V libovolném okolí bodu a (i jednostranném) najdeme jak racionální, tak iracionální čísla, takže na tom okolí d osciluje mezi 0 a 1. Protože tato oscilace nejde zmenšit tím, že zmenšujeme okolí, není v a žádná limita, ani jednostranná.

Protože nemáme limity, nemůžeme ani mít spojitost (ani jednostrannou), takže Dirichletova funkce není spojitá v jediném bodě. Proto také nemáme derivace, ani jednostranné.

Není také žádný bod, kde by tahle funkce byla monotonní. Vezměme nějaké a, třeba racionální. Pak d(a) = 1 a v libovolném okolí máme iracionální čísla, kde d = 0, napravo i nalevo od a, což znemožní jakoukoliv monotonii. Podobný argument funguje pro iracionální čísla. Proto také není interval, kde by byla funkce monotonní. Podobně se nahlédne, že není interval, kde by byla funkce konvexní či konkávní.

Další zajímavá vlastnost je, že d je r-periodická pro každé kladné racionální číslo r. Zvolme takové r. Jestliže je x racionální, pak x + r je také racionální, proto d(x + r) = 1 = d(x); jestliže x je iracionální, pak x + r je také iracionální a d(x + r) = 0 = d(x) jak požadováno.

Na druhou stranu, tato funkce není q-periodická pro q iracionální. Například 0 je racionální, proto d(0) = 1, ale 0 + q = q je iracionální, takže d(0 + q) = 0, což není rovno d(0).

V této poznámce dokážeme, že tato funkce není Riemannovsky integrovatelná na žádném intervalu.

Modifikace 1

Definujeme

Tato funkce vypadá takto:

Tentokráte jsme nenakreslili souvislé linie, ale vytečkovali jsme je, abychom naznačili roztříštěnou podstatu grafu, tento obrázek je ale stejně nepřesný jako ten první se spojenými čárami, protože musíme pamatovat, že v grafu nejsou žádné díry, jak je teď kreslíme, co se nám zdá jako díry je vlastně plné teček. V racionálních číslech tyto tečky leží na přímce y = x, iracionální tečky leží na nulové úrovni. Tato funkce má limitu v počátku, je tam dokonce spojitá, ale není tam diferencovatelná, protože směrnice odpovídajících přímek osciluje mezi 0 a 1 (detaily jsou stejné jako podobný příklad v sekci o "pilovitých" funkcích).

Modifikace 2

Definujeme

Tato funkce vypadá následovně:

Zde tečky odpovídající racionálním číslům sledují parabolu, zatímco iracionální tečky jsou zase na nulové úrovni. Mimo nulu je tato funkce stále stejně špatná jako Dirichletova, ale teď dokonce máme derivaci v počátku, jmenovitě f ′(0) = 0.

To zase ukazuje, že existence derivace v bodě nezaručí, že funkce bude pěkná, ani na malinkém okolí dotyčného bodu.

Modifikace 3

Definujeme

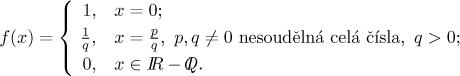
Tato funkce se se dost liší. V iracionálních číslech je nulová, ale v ostatních bodech je to jiné. Abychom si to mohli lépe představit, zkusíme se podívat na hodnoty v rozličných bodech. Abychom si to ulehčili, nejprve ukážeme, že tato funkce je 1-periodická.

Jestliže x je iracionální číslo, pak x + 1 je také iracionální, proto f (x + 1) = 0 = f (x). Jestliže x je racionální, pak jej napíšeme jako p/q pro nesoudělná celá čísla jako v definici funkce. Pak x + 1 = (p + q)/q s p + q, q nesoudělnými, takže jde o správné vyjádření a platí f (x + 1) = 1/q = f (x).

Proto je tato funkce n-periodická pro všechna přirozená čísla n. Toto jsou ale jediné periody. Stejně jako u Dirichletovy funkce se ukáže, že iracionální čísla nejsou periody, teď dokonce necelá racionální čísla nejsou periodami. Zvolme nějaké r = p/q s q > 1 a p, q nesoudělnými. Uvažujme x = −r. Pak f (x + r) = f (0) = 1, zatímco f (x) = 1/q < 1. Proto r nemůže být perioda.

Když máme periodicitu udělanou, víme, že stačí znát, jak vypadá graf na intervalu ⟨0,1⟩. Víme, že v iracionálních bodech dostáváme nulu, co další body? Máme f (1/2) = 1/2, f (1/3) = f (2/3) = 1/3, f (1/4) = f (3/4) = 1/4, f (1/5) = f (2/5) = f (3/5) = f (4/5) = 1/5. Jak si to představíme? Jak bereme větší a větší přirozená čísla n, dostáváme více a více čísel ve tvaru k/n a tečky odpovídající hodnotám funkce v těchto bodech klesají.

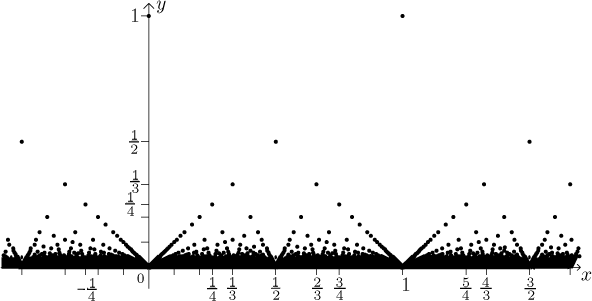
Jak se díváme níže, blíže k ose x, je tam stále více a více bodů, takže z grafu se stává docela zmatek.

Jaké jsou vlastnosti této funkce? Ať se to zdá sebepřekvapivější, v libovolném bodě a máme limitu, jmenovitě nulu. Protože jde o základní vlastnost této funkce a zní trochu neuvěřitelně, na konci sekce ukážeme v Příloze důkaz.

Z toho pak vyplývá, že tato funkce je spojitá ve všech bodech, kde má hodnotu nula, proto je f spojitá ve všech iracionálních bodech a nespojitá ve všech racionálních bodech. Protože tam máme limity, vidíme, že tyto nespojitosti jsou všechny odstranitelné. Tohle všechno je tak podivné, že to bude asi nejlepší závěr naší zoo příšerek.

Příloha

Zde dokážeme, že pro každé a má funkce f limitu 0 v a. Předpokládejme tedy, že je nám dána tolerance ε > 0. Potřebujeme najít nějaké prstencové δ-okolí bodu a tak, aby na tomto okolí hodnoty f zůstaly v rozmezí ε od limity, tj. od nuly. Toto δ najdeme následovně.

Nejprve najdeme nějaké přirozené číslo r tak, aby 1/r < ε. Množina zlomků, které leží do vzdálenosti 1 od a a jejichž jmenovatelé (v základním tvaru) nepřesáhnou r je konečná množina, proto existuje nějaké δ takové, že žádný z těchto zlomků neleží v odpovídajícím prstencovém δ-okolí bodu a. Poznamenejme, že a samotné může být jeden z těchto zlomků, ale v limitě ignorujeme limitní bod a samotný, takže na tom nezáleží.

Je toto δ to pravé? Zvolme nějaké x z tohoto okolí. Jestliže je x iracionální, pak f (x) = 0, proto jistě | f (x)| < ε. Jestliže je x racionální, pak jej napíšeme v základním tvaru jako p/q. Protože to nemůže být jeden z těch zlomků, které jsme vyloučili, musí být q > r, proto

| f (x)| = 1/q < 1/r < ε.

Důkaz je hotov.

Zpět na Teorie - Elementární funkce