sin(1/x) a spol.

Tato sekce je vlastně jakýsi souputník předchozí sekce, "pilovité" funkce. Ukážeme funkce, které mají podobné chování, jako příklady v oné sekci, ale budou "hladké" neboli všechny příklady budou diferencovatelné, kolikrát chceme, v bodech mimo x = 0.

Příklad 1

Uvažujme následující funkci:

Co můžeme o této funkci říct? Víme, že osciluje mezi −1 a 1. Její nulové body jsou 1/(kπ) a tvoří posloupnost jdoucí k 0. Protože vlny sinu jsou mezi těmito body, vyplývá z toho, že vlny se stále více a více zahušťují směrem k počátku, graf vypadá takto:

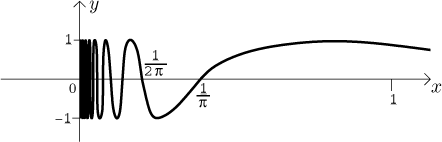
Všimněte si, že máme nekonečně mnoho vln, funkce nikdy nepřestane oscilovat mezi −1 a 1, jak se blížíme k počátku, takže z toho vyplývá, že není žádná limita v 0 zprava. Na druhou stranu má funkce pro x > 0 všechny derivace.

Příklad 2

Uvažujme následující funkci:

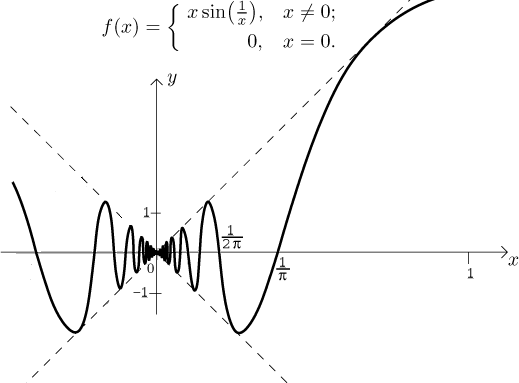
Pořád tady máme onu nikdy nekončící oscilaci jdoucí k počátku, ale teď je její amplituda modifikovaná členem x, z čehož vyplývá, že tato funkce má limitu rovnou 0 v x = 0. Protože to se shoduje s definicí v 0, je tato funkce v počátku spojitá. Je tedy spojitá všude a pro nenulové x má také všechny derivace. Nemá nicméně derivaci v 0. Odůvodnění pro tento závěr je podobné jako v sekci o "pilovitých" funkcích; když konstruhujeme přímky aproximující tečnu a jdeme k počátku, směrnice kolísají mezi −1 a 1 a nikdy se neusadí. Závěr:

Příklad 3

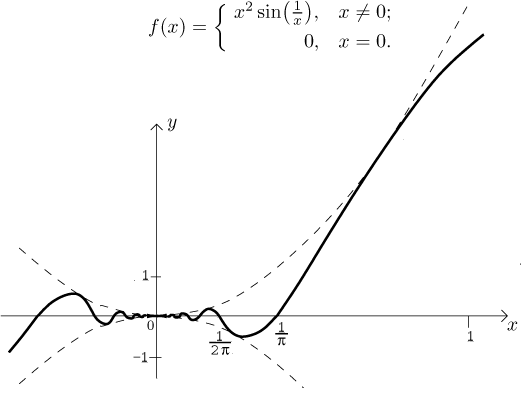
Zase tu máme funkci spojitou všude a diferencovatelnou kolikrát chceme v nenulových bodech. Tentokrát ale máme i derivaci v počátku, odůvodnění je zase stejné jako u odpovídající funkce z "pilovitých" funkcí, ale tentokráte je také možné spočítat derivaci v nule relativně stadno z definice. Máme tedy

Ověřte si limitou, že tato první derivace není spojitá v počátku. To tedy ukazuje, že existují funkce, které jsou sice všude diferencovatelné, ale ta derivace není spojitá. (srovnej Derivace: základní vlastnosti v části Derivace - Teorie - Úvod). Má ale vlastnost mezihodnoty.

Stejně jako u předchozího příkladu se dá dokázat, že druhá derivace této funkce v počátku neexistuje. Obecně můžeme zvolit nějaké přirozené číslo n a uvažovat následující funkci:

Tato funkce je spojitá na reálné ose, má všechny derivace v nenulových x a její derivace v x = 0 je rovna nule až do řádu (n − 1), ale neexistuje n-tá derivace v počátku.

Dirichletova funkce
Zpět na Teorie - Elementární funkce