Polynomials and rational functions

Definition.
By a polynomial we understand any function of the form

p(x) = a₀ + a₁x + a₂x² +...+ a_nxⁿ,

where a_k are real numbers.
Consider a polynomial p(x) = a₀ + a₁x + a₂x² +...+ a_nxⁿ. We define the degree of p, denoted deg(p), as the largest index k such that a_k ≠ 0.

The fact that a_k are real is sometimes emphasised by using the name "real polynomial". There are also other polynomials, for instance "complex polynomials" arise when we allow a_k to be complex numbers. However, here we will only work with real functions, and so we just say "polynomials" and mean real polynomials.

The numbers a_k are called coefficients. Some of them may be zero, which means that the expression above is not unique for a given polynomial. For instance, we can have p(x) = 1 + 2x² = 1 + 0x + 2x² = 1 + 2x² + 0x⁵. By the above definition, the degree of this polynomial is 2, and it is customary to leave out the powers that are higher than the degree and thus do not really appear; that is, the last expression would be used only exceptionally. The highest power that really is a part of a polynomial - the power that defines its degree - plays an important role in its behaviour and we call it the leading power. Therefore people often write polynomials in the opposite order, from the highest to the lowest power. Note that polynomials of degree 0 are exactly the non-zero constant functions, p(x) = a₀.

What is the degree of the zero polynomial (or constant zero function)? The most popular choices are −∞ and −1, depending on which popular facts about degrees you want to be true also for zero polynomials. Given the ambiguity, some authors prefer to leave the degree of zero polynomial undefined. By the way, the choice −1 makes the following statement work for all polynomials including the zero one: Let k be the smallest non-negative integer such that k-th derivative of p is zero. Then k − 1 is the degree of a p.

We often use the phrase "let p(x) = a_nxⁿ + a_n−1xⁿ⁻¹ +...+ a₁x + a₀ be a polynomial of degree n"; then it follows that the coefficient a_n is not zero.

The degree of polynomial satisfies the following properties:
(i) deg(p⋅q) = deg(p) + deg(q);
(ii) deg(p + q) ≤ max(deg(p),deg(q));
(iii) if deg(p) > deg(q), then deg(p + q) = deg(p).

These formulas are definitely true for non-zero polynomials. Their general validity dependas on how we define the degree of the zero polynomial. If we set it to −∞ then all three statements will be valid in general, which explains why this choice is popular. If we set it to −1, then only the last two will work. As a curiosity we remark that the choice ∞ works with the first two formulas.

In most situations it is enough to consider only polynomials with a_n = 1, since we can always write

p(x) = a_nxⁿ + a_n−1xⁿ⁻¹ +...+ a₁x + a₀ = a_n[xⁿ + (a_n−1/a_n)xⁿ⁻¹ +...+ (a₁/a_n)x + a₀/a_n] = a_n⋅q(x).

The polynomial q is of the same degree as p and the most important properties of polynomials are the same for p and q, so it is often enough to investigate q (and it has the coefficient at the highest power equal to 1).

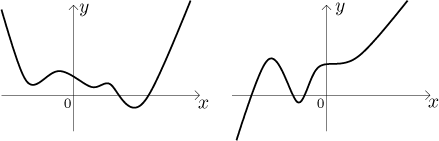
Shape of a polynomial.

For understanding polynomials it helps to know that when x gets close to infinity (or negative infinity), then the leading term will win over the other terms - they become unimportant. Thus a polynomial of degree n has shape very similar to a_nxⁿ around "the ends", for very large (in absolute value) values of x. This can be very useful in many situations. Since we know how powers xⁿ look like (see the previous section), we can make a good guess about shapes of polynomials.

These are the typical shapes for polynomials of even degree (on the left) and odd degree (on the right), assuming that there is a positive coefficient at the highest power.

If there is a negative coefficient (like in the polynomial −2x³ + 5x + 1), the shape gets flipped around the x-axis:

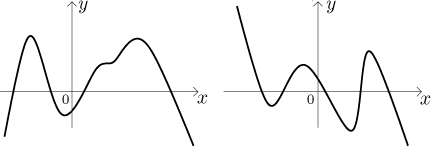
How many "bends" are there for a polynomial p? At most deg(p) − 1. For instance, a polynomial of degree 2 always has exactly one bend, since its graph is the parabola.

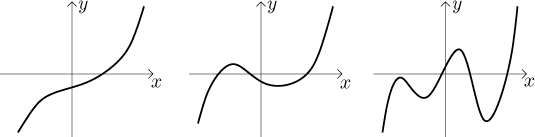
From the typical shape it also follows that a polynomial of odd degree must have an even number of bends, since its "ends" at infinity and negative infinity always point in the opposite directions. On the other end, polynomials of even degree have "ends" pointing the same way, so they must have an odd number of bends. Thus for instance a polynomial of degree five can have these basic shapes:

The name linear function denotes any function of the form f (x) = kx + b, where k,b are arbitrarily chosen fixed constants. Linear functions are therefore polynomials of degree at most 1. They are exactly those functions whose graphs are lines. If k = 0, then the graph is a horizontal line at the level b, in this way we get constant functions. Otherwise we get lines that go up or down, depending on k. The coefficient k is called the slope of the corresponging line and it gives the steepness of its rise/descent. One popular value is k = 1, when the line goes up at the angle π/4 radians (45 degrees). The constant b gives the y-intercept.

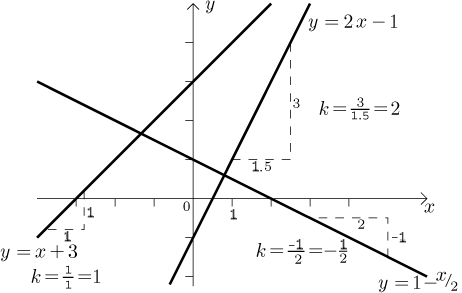
The angle at which the line goes up/down is given by the formula α = arctan(k). This can be also taken as a formula for k, tan(α) = k, but usually it is better to find k using triangles. Take an arbitrary triangle as indicated in the picture, find its height y and base x, then k = y/x.

The ability to quickly pass from a linear function to its graph and from a picture of a line to the formula that gives it is very useful, since linear functions belong among the most useful functions and appear very often.

How many roots can we have for a non-zero polynomial p? Recall that by a root we mean a number c such that p(c) = 0. Theory says that there can be at most deg(p) roots. This can be guessed from the shape of the graph. For instance, the graph of a polynomial of degree 5 might have these positions:

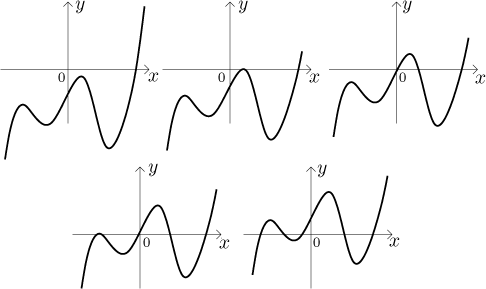
We see that it can have between 1 and 5 roots. In fact, polynomials of odd degree have always at least one real root.

Sidenote: The claim about number of roots would be true for all polynomials only if we decided that the zero polynomial has degree infinity, but that would play such a havoc with other properties that people do not do it.

In complex numbers, polynomials are better behaved. We will therefore briefly look at complex things, but we will quickly get back to reals. Note that real polynomials are also complex polynomials, since real numbers are a subset of complex numbers. Thus given a real polynomial, one can substitute complex numbers for x and pretend that it is a complex polynomial, drawing on some properties. We start right away with the main result.

This Fact works in general for complex polynomials and complex roots, but if we start with a real polynomial and a real root, then the new polynomial q will be also real.

If we work in complex numbers, then we start with the Theorem, apply the Fact on factorization, and if the new polynomial q is not a constant, we can return to the Theorem and factor it further and so on, so we get

Corollary (factorization of polynomial to linear factors).
Let p(x) = a_nxⁿ + a_n−1xⁿ⁻¹ +...+ a₁x + a₀ be a polynomial of degree n > 0. Then there are complex numbers c₁,c₂,...,c_n which are all roots of p and satisfy

p(x) = a_n(x − c₁)⋅(x − c₂)⋅...⋅(x − c_n).

Thus every non-zero polynomial has exactly as many complex roots as its degree (this also fits for degree zero), but some of these roots may be the same. When we put the corresponding roots together, we can rearrange the above decomposition into

p(x) = a_n(x − c₁)⋅(x − c₂)⋅...⋅(x − c_n) = a_n(x − d₁)ⁿ⁽¹⁾⋅...⋅(x − d_N)^n(N).

Now d_i are distinct roots of p. Each corresponding power n(i) is called the multiplicity of the root d_i (see this note). For example, we may have

p(x) = (x − 1)⋅(x − 1)⋅(x − 3) = (x − 1)²⋅(x − 3).

We would say that 1 is a root of multiplicity 2, while 3 is a root of multiplicity 1, also called a simple root.

Note that having such a nice decomposition with real coefficients is a matter of luck, since in general we are only guaranteed complex roots. Since we are only interested in real polynomials, we will now try to deduce some useful information that would not use complex numbers.

Fact.
If c is a complex root of a real polynomial p, then its complex conjugate is also a root of p.

This is wonderful, because it means that when we start factoring the polynomials, for every term (x − c) we also have (x − c*).

Fact.
For a complex number c and its conjugate c* we have (x − c)⋅(x − c*) = x² + ex + f, where e and f are real numbers.

Thus when we start with a real polynomial, we may get complex roots, but their factors can be put together in pairs to create real quadratic polynomials. Therefore we get

In this decomposition, the linear terms (x − d_i) correspond to real roots of p, the quadratic terms (x² + e_jx + f_j) arise from complex roots. They are irreducible, which means that they cannot be further factored into (x − a)(x − b) using real numbers. Indeed, if such a factorization were possible, then such a quadratic term would have two distinct complex roots which created it and also a third (real) root a, which is impossible for a polynomial of degree two.

Such factorization can be very useful, and we see that having it is equivalent to knowing the roots of p. Unfortunately, finding such a factorization is generally next to impossible. Everybody and his dog knows the famous quadratic formula for finding roots of quadratic polynomials. There are also formulas for finding roots of cubic polynomials (degree 3), but they are not very pleasant and nobody remembers then anyway. Formulas for roots of polynomials of degree 4 are so ugly that most books actually skip them so as not to traumatize the more delicate reader. To top it off, one of major results of general algebra is that for polynomials of degree 5 and more there cannot exist any formula for roots.

Finding roots is thus a matter of chance and luck. Usually we try to guess one root, then take out the corresponding factor (x − c) and check of the resulting polynomial whose degree is smaller by 1 than the original one.

Example: We try to factor p(x) = x⁶ − 3x⁴ + 2x³.

Solution: We see that

p(x) = x³⋅[x³ − 3x + 2] = (x − 0)³⋅[x³ − 3x + 2].

Thus we see that 0 is a root of p of multiplicity 3. What about q(x) = x³ − 3x + 2? This is a cubic polynomial, so there are formulas for roots, but we do not remember them. However, this being a textbook example, we hope that some nice root will exist, namely an integer that is not too large. So we start substituting in 0, 1, −1, 2, −2,... and we soon find that 1 is in fact a root. We divide:

(x³ − 3x + 2)/(x − 1) = x² + x − 2.

We obtained a quadratic polynomial, whose roots are 1 and −2 by the quadratic formula. Thus 1 is actually a root of multiplicity 2 and −2 is a simple root. We get

p(x) = (x − 0)³⋅(x − 1)²⋅(x − (−2)) = x³⋅(x − 1)²⋅(x + 2).

Note: Instead of using the quadratic formula, one can also try to guess the factorization, see this remark.

Example: We try to factor p(x) = x³ + 3x² + 3x + 2.

Solution: We try to guess, after a while we find that p(−2) = 0. We divide:

(x³ + 3x² + 3x + 2)/(x − (−2)) = (x³ + 3x² + 3x + 2)/(x + 2) = x² + x + 1.

The quadratic formula shows that x² + x + 1 does not have any real roots, so the best possible factorization is

p(x) = (x + 2)⋅(x² + x + 1).

Example: We try to factor p(x) = x⁴ + x² + 1.

Solution: We try to substitute 0, 1, −1, 2, −2,..., but after a while we give up. What can we do? Since guessing did not help, this problem is not solvable by tools we know.

Note that the only irreducible polynomials are those of degree 1 (linear) and 2 (quadratic), so there must be some factorization of p. Perhaps there are real roots, but they are not integers so we can't guess them. Since the polynomial is of even degree, it might also happen that there are no real roots. In fact, that is exactly what is happening here, we have

p(x) = (x² + x + 1)⋅(x² − x + 1).

How did we get it? We cheated, we created this example by starting with two irreducible quadratic polynomials and multiplied them together. If we did not know the answer from the very start, we would not know how to solve it.

Now we look at a different topic, related to factoring. We used the long division of polynomials, in general one gets a remainder when dividing. To show some motivation we recall the following: When we try to divide 17 by 5, we get answer: It is 3, with remainder 2. We could write it as follows: 17 = 3⋅5 + 2, another way is 17/5 = 3 + 2/5. For the moment we prefer the first way. How do we know that the remainder is 2 and not, say, 7, since we can also write 17 = 2⋅5 + 7? For the remainder there is a simple rule: It is a non-negative number r such that there is an integer s with 17 = s⋅5 + r and r < 5. With this definition it is clear that 2 is really the remainder, no other integer would work.

Remarkably, one can do the same for polynomials, instead of the magnitude of number we will use the degree of polynomial.

Fact (division with remainder).
Let p,q be polynomials. Then there are unique polynomials s,r such that

p(x) = s(x)⋅q(x) + r(x)

and deg(r) < deg(q).

Again, one can express it as p/q = s + r/q. This will come handy momentarily.

Sidenote: We have no restrictions on p and q in our theorem, so one or both may be the zero polynomial. This fact remains true as long as we define the degree of zero polynomial to be negative, so the popular values −∞ and −1 are fine here.

By a rational function we mean any ratio p/q of polynomials. These functions are very popular. The domain of such a function is all real numbers except the roots of q(x). A rational function is called proper if deg(p) < deg(q).

Every rational function can be written as a sum of a polynomial and a proper rational function with the same denominator. This is just a reformulation of the Fact on division with remainder. In practice we do it using the algorithm for long division.

Since polynomials are relatively easy to handle, we see that in order to work with rational functions, in many situations it is enough to know how to work with proper rational functions. This is particular applies to the method of partial fractions decomposition. Since this method is very important, we dedicated a special section to it, and since the main use (at least for us) is for integration, we put that section there, so for partial fractions check out Integrals - Theory - Integration methods - Partial fractions.

Briefly, the method first calls for breaking the denominator q into linear and quadratic (if needed) factors as we discussed above, the proper rational function can be then broken into a sum of simple so-called partial fractions, very simple fractions whose denominators come from the linear and quadratic factors of q. A practical point of view is here.

One last note: When talking about polynomials we remarked that when x is close to infinity (or negative infinity), then a polynomial is essentially equal to its leading term. Therefore when p(x) = a_nxⁿ +... is a polynomials of degree n and q(x) = b_mx^m +... is a polynomials of degree m, then the rational function p/q is for large (in absolute value) x pretty much equal to (a_n/b_m)x^n-m. This fact can come very handy.

Exponentials, logarithms
Back to Theory - Elementary functions