Int(x) and Frac(x)
Definition.
Let x be a real number. We define its integer
value as the largest integer Int(x) satisfying the
condition
Int(x) ≤ x.
We define its fractional value as
Frac(x) = x − Int(x).
Examples: Int(3) = 3,
Frac(3) = 0;
Int(0.14) = 0,
Frac(0.14) = 0.14;
Int(17/8) = 2,
Frac(17/8) = 1/8 = 0.125;
Int(85263.781235) = 85263,
Frac(85263.781235) = 0.781235.
Now it gets more interesting: Int(−1) = −1,
Frac(−1) = 0;
Int(−2.15) = −3 (really,
−3 is the largest integer that is not larger than
−2.15),
Frac(−2.15) = 0.85;
Int(−135.643) = −136,
Frac(−135.643) = 0.357;
Int(−117) = −117,
Frac(−117) = 0.
You probably ask, why don't we define Int(x) as whatever is in front
of the decimal point and Frac(x) as whatever is after the decimal
point. Good question, I would like it that way, too. Unfortunately, such a
definition would sometimes cause troubles, whereas the
funny one that we put here is - from the mathematical point of view - without
problems. One advantage we can show right away: The "right" definitions give
much nicer graphs:
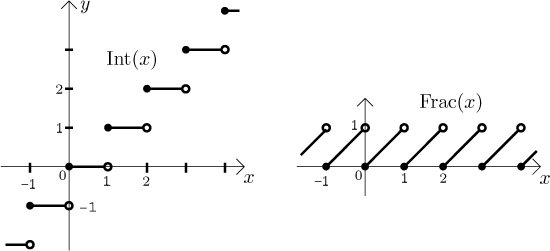
In fact, since we mostly use these functions for positive numbers, many
people are not even aware that the definition behaves funny for negative
numbers.
There is another justification for this definition. We can say that
Int(x) is actually x rounded down to the nearest
integer. There is also an alternative notation,
Int(x) = ⌊x⌋.
Similarly one can define ⌈x⌉ as
x rounded up to the nearest integer.
Examples:
⌊13⌋ = 13,
⌈13⌉ = 13;
⌊13.7⌋ = 13,
⌈13.7⌉ = 14;
⌊−23⌋ = −23,
⌈−23⌉ = −23;
⌊−23.6⌋ = −24,
⌈−23.6⌉ = −23.
Factorial
Back to Theory - Elementary functions

