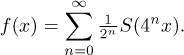"Saw-like" functions

In this section we will look at some functions from the "freak zoo" that will serve as a warning that some ideas, although they may look true when we consider "nice" pictures, in fact do not work. There are many such useful "counter-example" functions, here we will look at those that have some "saw" idea in them.

Example 1

Consider the following function on the interval (0,1]. First we take the interval [1/2,1] and erect a regular "tooth" of height 1/2 above it, that is, imagine an isosceles triangle with base [1/2,1] and height 1/2. Next, we look at what is left of (0,1], namely (0,1/2), and take the right half of it. On the interval [1/4,1/2] we erect another "tooth" of height 1/2. Then consider what is left, (0,1/4), and erect a "tooth" of height 1/2 over its right half, [1/8,1/4]. We continue in this manner, eventually (after infinitely many steps) we will make teeth over the whole interval (0,1].

The function we thus obtained is continuous on (0,1], it is

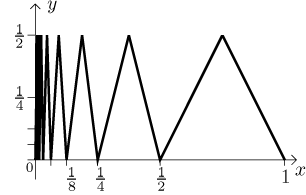
Modification 1:. At every step we make a tooth as before, but we will make its height to be half of the previous height, so the first tooth has height 1/2, the second 1/4, etc. In fact it so fits that when making a tooth over a certain interval, its height is the same as the left end of the interval (check).

This function, call it f, satisfies | f (x)| ≤ x, therefore by the Squeeze theorem it has a limit at 0 from the right, namely 0 (it should be clear from the picture). Thus we can define also f (0) = 0 and we get a function on [0,1] that is continuous.

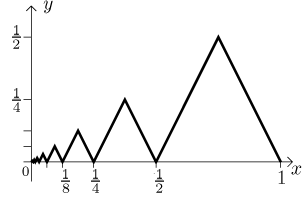
By the way, if we want to be precise (this will be used below), we can show that the tops of the teeth in fact lie on the line y = (2/3)x.

Now we take this example and "mirror it" to the interval [−1,0] symmetrically with respect to the origin, that is, we flip the graph about the y-axis and then about the x-axis. We will still call it f since this is just an extension of the previous picture.

This function is continuous and odd on [−1,1], note that it is non-decreasing at 0, but there is no interval at all on which this function is monotone that would include 0 in its interior. No matter which interval (a,b) you take, if you have a < 0 and b > 0, then this interval will include some tooth, which means that the function will be going up at some places and going down at other places within (a,b), contradicting any monotonicity there.

Note also that this function does not have a derivative at the origin, although the function is continuous and monotone at x = 0. Indeed, take some non-zero y and consider the line conecting the origin and the point (y, f ( y)). What happens to the slope of this line as we send y to 0? No matter how close to 0 we get, we will always have some values even closer where the teeth hit the x-axis, that is, where f ( y) = 0, then the slope will be 0. On the other hand, there will always be the tips of teeth as well, where the slope is 2/3 (see the note about the line above). Thus as we send y to 0, the slopes keep oscillating between 0 and 2/3 and no limit is possible.

Modification 1*:. In the above picture the tops of teeth followed the line y = 2x/3. We can modify the definition so that the tops of teeth follow, for positive x, the parabola y = x², on the negative half we again mirror the positive part:

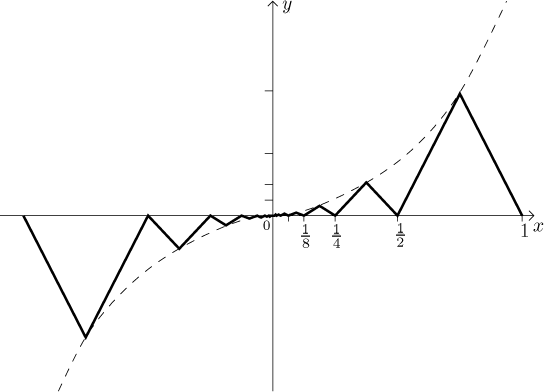
This function has similar properties as the one in Modification 1, but now it also has a derivative at x = 0, it is equal to zero.

Modification 2: Take the function from Modification 1 and make a little change: switch every second tooth (counted from the ends) about the x-axis.

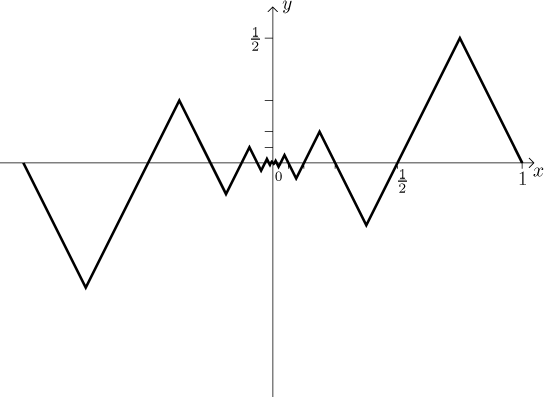
Again, we have a continuous and odd function on [−1,1] without a derivative at 0, but this time we also do not have any monotonicity at 0.

Example 2

Well, this is not really a "saw-like" function, but it follows readily from the previous example. Take the function f from Modification 1 and make the following change (we will describe the right half, the left one is symmetric): Consider an interval I over which a tooth has been erected (like [1/2,1], [1/4,1/2], etc). Instead of a tooth, draw a horizontal line at the level of the tip of the tooth, but only over the right half of this interval (where the tooth was going down), and a horizontal line at the quarter of the level of the tooth tip over the left half (where the tooth was going up). Fill in the ends that are closer to the origin (and the very outer ends as well).

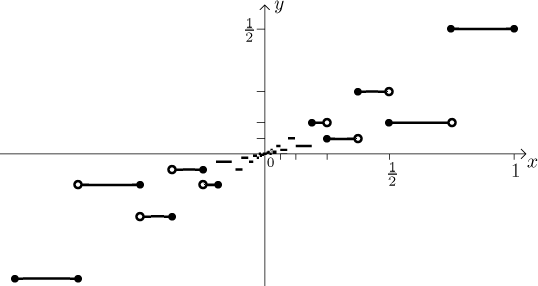
This is an interesting function. Note that still | f (x)| ≤ |x| for all x from [−1,1], so in particular the function has a limit 0 at x = 0, therefore it is continuous at 0. This function is also monotone at 0, this time it is actually (strictly) increasing.

However, there is no interval around the origin (an interval that would include the origin in its interior) on which the function is monotone and there is also no such interval on which the function would be continuous. This shows that monotonicity and continuity at a point do not imply that there would be some interval around on which the function would be "nice" (monotone or continuous).

Also in this example there is no derivative at 0. It is not difficult to show that this time, the slopes of the corresponding lines oscilate between 2/3 and 1/6.

Also this example can be fixed so that it has a derivative at the origin (see the above Modification 1*). We get a function that has a derivative at the origin, but there is no neighborhood of the origin on which the function would be continuous or monotone. Especially the continuity part is sad, we see that the existence of derivative at a point does not force the function to be nice a bit around. In case you care, we include some detils about the construction. In Modification 1* we made the segments in pairs and the right one (the "top" one) had its left end on the curve y = 2x/3 (for positive <x, the left half of the graph was symmetric). The modification is that now we make the pairs so that the "top" segments (of the right half of the graph) have their left ends on the curve y = x², each "low" segment is now the level of one-sixth of the level of the corresponding "top" segment.

Example 3

Now we try something different. We will create a function on [0,1] that is not bounded. The idea will be similar. First, make a tooth of height 1 over [1/2,1]. Then make a tooth of height 2 over [1/4,1/2]. Then make a tooth of height 4 over [1/8,1/4]. Continue in this manner, each time doubling the height of the tooth. Eventually we cover (0,1], so it remains to define the function at 0. We can do it any way we feel like, for instance we can set the value at 0 to be 1 (the picture is so crowded we won't see it anyway).

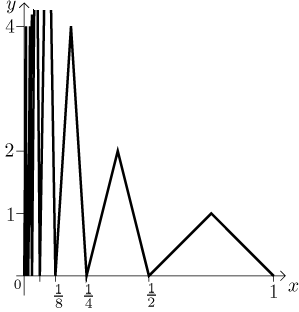
This function is defined on a bounded interval [0,1], but it is not bounded above, only from below.

If we do a slight modification and make every second tooth going down, we get a function that is not bounded from below either.

Example 4

Here we will use infinite sum to create a function on ℝ. We start with a simple regular "saw", this will be our function S:

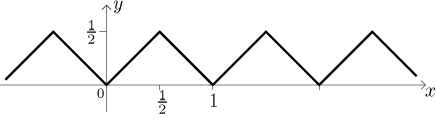
The second function will be S scaled down four times, and then multiplied by 2, let's call it S₂:

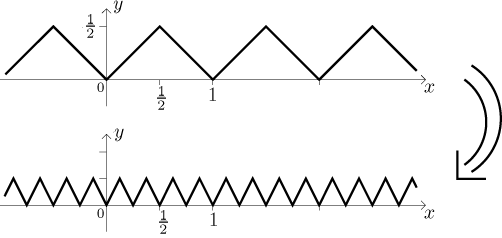
Thus every tooth is made into four teeth whose height is half of the original height. Note that thus these teeth are twice as steep. Mathematically we can write S₂(x) = S(4x)/2. Note that both these functions are 1-periodic and the same will be true about all others, so we will further focus on one period.

In the next step we create S₃ by scaling down S₂ four times and then multiplying by 2:

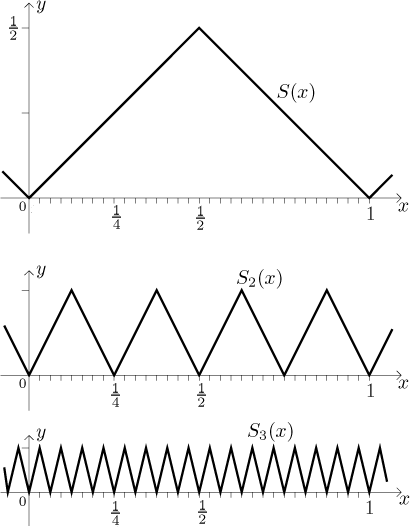
Now S₃(x) = S₂(4x)/2 = S(4²x)/2².

We continue in this manner, obtaining functions S_n(x) = S(4ⁿx)/2ⁿ. What happens if we add these functions? This takes a bit of work (see Function series in Series - Theory), but one can show that the infinite sum of these functions makes sense (converges) and yields a continuous function. Thus we can define

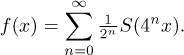
How does it look? We still draw just one period:

When we add S₂ to S, we get this:

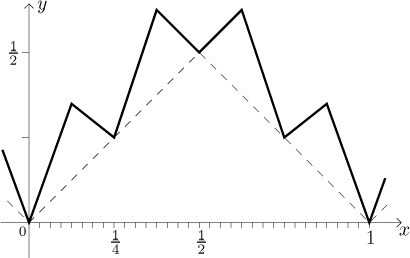
Note several things. First, on every flat part of the graph of S two pyramids grew. Second, the function S did not have any derivative at points of the form k/2, and now, after adding S₂, the sum does not have derivative at any point of the form k/(2⋅4) = k/8.

Now we add S₃.

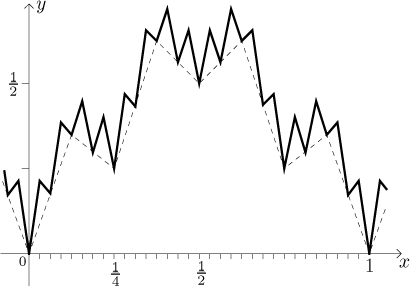
Note that the trends are still there. Two pyramids grew on every flat face and there are no derivatives at points of the form k/(8⋅4) = k/32. After adding S₄ we get

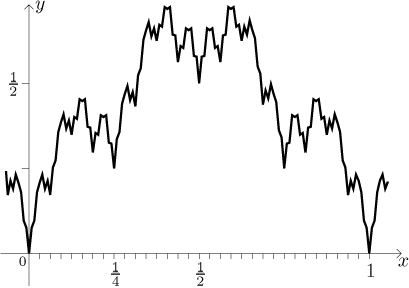
We continue in this manner and obtain the function f. Since the pyramids are getting thinner and thinner, we are soon unable to draw the graph properly, the best we can do is to say that it is sort of like the pyramid above, but somewhat fuzzy. What is more important, it can be proved that by adding further pyramids, the "breaking" points of the lines, where we did not have derivatives, do not get fixed. Threfore, the function f does not have derivatives at points of the form k/2ⁿ. But this is quite bad, because points of this form are dense on the real line, they are everywhere. Consequently, we have a function continuous on the whole real line, but there is not a single non-degenerate interval on which this function would be differentiable.

Interestingly, mathematicians used a similar idea to create a monstrous function that is continuous on the real line, but does not have any derivative anywhere, it does not even have proper one-sided derivatives! Hard to imagine, but now we can at least believe it. In fact, the construction is just like the one above, we start with the same S and then we add S_n(x) = S(100ⁿx)/10ⁿ. Why didn't we show this function right away? Since we could not draw it as well, notice that already S₂ has 100 tiny pyramids in the interval (0,1).

sin(1/x) a spol.
Back to Theory - Elementary functions