
The most popular unit for measuring angles is the degree. There is 360 degrees to a full circle, 90 degrees is the right angle. There are essentially two ways of specifying the angle between two rays.
1. If the rays are of the same importance, we get an angle that is not oriented (for instance between the sides of a triangle). Given two rays, we always take the smaller angle, measure it and express the answer as a positive number (or zero).

2. If one ray is in some way special (for instance the x-axis in a coordinate system), we usually use an oriented angle, taken positive in the counterclockwise direction (towards the y-axis) and negative in the clockwise direction.
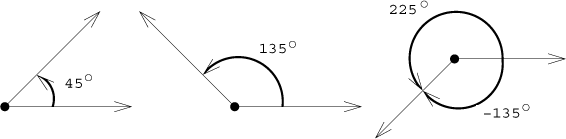
We see that now the same angle can be specified in several ways. In fact, it can be specified in infinitely many ways, since in this situation we can go around the origin several times, each time gaining a full circle (360 degrees), and we can do it both ways.
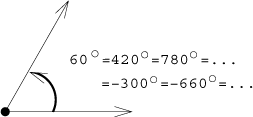
Degrees are "practical". People use them when working with geometrical objects, calculating distances and angles "in the real world" and situations like this. Since they correspond to directions on a compass, we are pretty familiar with them. In such settings we also often use the non-oriented angle.
However, in sciences, most notably in math and physics, we (almost) always use the oriented angle and prefer a different unit for it: the radian.
Given an angle, we obtain its size in radians by dividing the arc length by the radius.
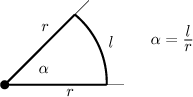
This is one great advantage of the radian, since in situations as in the
picture we calculate the arc length as
The full angle is (circumference)/(radius), that is, the full angle is
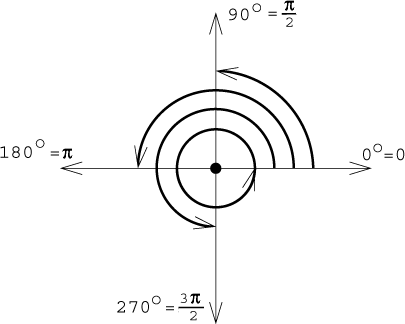
The relationship between degrees and radians is linear, so we have simple transformation formulas:
![]()
Probably the most popular angles are these:
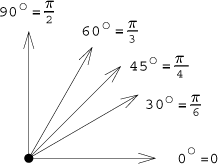
Why are they popular?
Note that if we make a right-angle triangle with another angle
By adding/subtracting right angles we get the whole "compass rose":
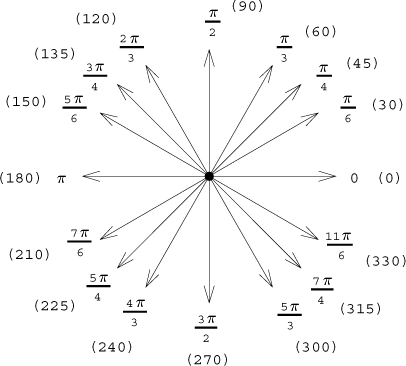
Since the two units are tied linearly, one can use any of them for
measurement with no trouble. However, things change when we start using these
measurements in calculations. In particular, we have to be careful how we
substitute angles into trig functions. The tables of, say, sine are different
for angles measured in degrees and for angles measured in radians. For
instance, if we have sine that expects radians, we get
For 90 degrees we need a different sine, the one that expects degrees. This is actually a popular source of errors in calculations, when a student forgets to switch his calculator into degrees (or radians, whichever is needed).
Thus "sine in degrees" and "sine in radians" are two entirely different
functions. In mathematics, physics and other sciences we need a precise
specification, so long time ago it was decided to stick with radians. As we
remarked, radians are better for scientific calculations, so this makes
perfect sense, and it actually gives much nicer formulas. For instance, for
derivative we have
In conclusion, remember that in calculus all trigonometric function only eat radians.