Definice limity

Zde uvedeme jeden z nejdůležitějších pojmů spojených s funkcemi: limitu funkce. Než ukážeme formální definici, zkusíme získat představu, co je to limita. V zásadě je to pokus zodpovědět následující otázky: Je-li dána funkce f a nějaký bod a, co se stane s hodnotami f, jestliže do ní začneme dosazovat čísla blízká a? Další možná otázka je tato: Jestliže zůstaneme blízko a, je možné aproximovat hodnoty f nějakým číslem s dostatečnou přesností?

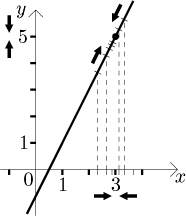
Uvažujme funkci f (x) = 2x − 1 a bod a = 3. Když dosazujeme hodnoty x blízké a = 3, výsledky jsou blízké 5. Čím blíže je x ke 3, tím blíže je f (x) k 5. Jinak řečeno, pokud nasadíme na osu x šoupátko, začneme ho posunovat směrem k a (z obou stran) a podíváme se, co dělají odpovídající hodnoty f, vidíme, že jdou do 5.

Toto chování se popíše slovy "f konverguje k 5 pro x jdoucí k 3", nebo že "5 je limita funkce f pro x jdoucí k 3".

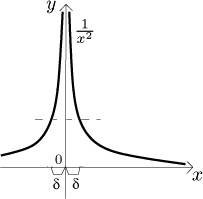
Měli bychom zdůraznit pár věcí, abychom hned v zárodku zažehnali několik častých nedorozumění ohledně limity. Za prvé, bod a se nebere v úvahu, když sledujeme hodnoty při hledání limity; je to jen cílový bod pro x, ty se k a přibližují libovolně blízko, ale nikdy se mu přesně nerovnají. Je dokonce možné hledat limitu v a, aniž by tam funkce vůbec existovala. V následujícím obrázku jsme oddělali a z definičního oboru f, ale pro limitu se nic nezměnilo.

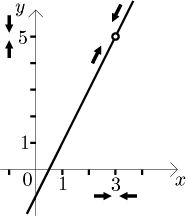
Jestliže chceme hledat limitu nějaké funkce f v jistém bodě a, je třeba jediné: V definičním oboru f musí existovat nějaká x, která se blíží libovolně blízko k a, takže má smysl říct "pro x jdoucí k a". Jestliže je nějaká funkce g definovaná na množině (0,1) ∪ (1,2), pak se nemá smysl ptát po její limitě v bodě 3, protože ta funkce vůbec neexistuje poblíž 3. Můžeme se ale ptát po limitě v bodě 1, protože se dá dojít libovolně blízko k 1 z obou stran pomocí čísel z oné množiny.

Existuje matematický pojem, který přesně vystihuje, co jsme právě napsali; řekli bychom, že a musí být hromadným bodem definičního oboru f. Mnoho autorů ale cítí, že to je příliš technické, a raději žádají trochu více. Jmenovitě, aby měla otázka na limitu v bodě a vůbec smysl, požadují, aby byla f definovaná na nějakém prstencovém okolí bodu a (v předchozím odstavci jsme uvaživali funkci g definovanou na prstencovém okolí 1). Tento požadavek je více omezující, ale také pohodlnější; ve většině případů navíc funguje, proto tento přístup zvolíme i zde v Math Tutoru. Volba přístupu je jen otázkou vkusu, pokud tedy otevřete nějakou učebnici a začnou tam mluvit o hromadných bodech, budete vědět, že to není zásadní rozdíl.

Druhá důležitá věc je, že ty obrázky nahoře byly příliš pěkné na to, aby daly správnou představu o limitě, protože ta funkce je neobvykle "pěkná" a také se k limitě blíží velice pěkně. Nic takového není potřeba. Tradiční vyjádření "limita znamená, že když se blížíme k a, pak funkce jde k L" je ve skutečnosti špatně právě proto, že naznačuje, že hodnoty by měli jít k limitě jaksi přímo, bez zacházek.

Ve skutečnosti funkce nemusí být vůbec spojitá (nebo třeba monotonní), a i když se funkční hodnoty k limitě blížit musí, mohou to dělat jakkoli bláznivě se jim zachce, jediná podmínka je, že se hodnoty f nakonec dostanou tak blízko, jak je požadováno, k limitní hodnotě. Zde nabízíme tento příklad, abychom ukázali, že k limitě se lze blížit i méně pěknými způsoby než výše, ještě ošklivější příklady lze nalézt v sekcích "pilovité" funkce, sin(1/x) a Dirichletova funkce v části Teorie - Elementární funkce.

Co se míní tím "nakonec...tak blízko, jak je požadováno"? Základní myšlenka je, že jsme ochotni tolerovat určitou odchylku (tradičně značenou epsilon ε), o kterou se f může lišit od limitní hodnoty, všimněte si, že to znamená, že hodnoty f musí zůstat ve vodorovném pruhu šířky 2ε okolo limitní hodnoty.

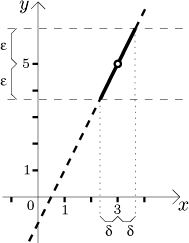
Evidentně nelze čekat, že se do této vzdálenosti vměstná celý graf; jak se blížíme (z obou stran) k a, tak hodnoty funkce mohou občas (nebo i často) vyskočit z tolerance. Aby ale limita platila, pak to vyskakování musí dřív či později skončit. Jinými slovy, musí existovat oblast okolo a, na které už hodnoty f již zůstávají v onom ε-pruhu okolo limitní hodnoty. Tato oblast okolo a je tradičně dána tak, že specifikujeme, jak daleko se můžeme od a vzdálit, aniž bychom s grafem vyskočili z pruhu, používáme pro to delta δ. Obrázek nahoře to asi vysvětlí nejlépe, další epsilon-delta situace je na konci toho méně pěkného příkladu.

Představte si to jako hru. Někdo vám dá epsilon, tedy toleranci, v typickém případě velice malé. Vaším úkolem je přinutit funkci, aby zůstala v odpovídajícím vodorovném ε-pruhu okolo (údajné) limitní hodnoty, a jediným nástrojem, který pro to máte, je možnost odříznout kusy grafu, které se vám nelíbí. Nemůžete ale odřezávat až u a, musíte nechat nějaký kousek grafu na obou stranách a, a vodorovná šířka toho grafu, který na obou stranách a necháte, je právě to delta, které máte najít. Pokud takové δ najdete, vyhráli jste tuto hru. Připomeňme, že hodnota v bodě a samotném se nebere v úvahu.

Tohle by ale nestačilo, abychom opravdu měli limitu. Klíčovým bodem je, že aby funkce opravdu měla žádanou limitu, musíme být schopni vyhrát všechny hry, ať už je to epsilon vybrané naším protivníkem jakkoliv malé. Přesvědčte se pohledem na první příklad a na ten méně pěkný, že v obou případech je možné vyhrát všechny hry, i pro velice malinké epsilon. Tedy krátce řečeno, aby byla limita pravdivá, musí se funkce dostat blízko k limitní hodnotě a dřív či později také blízko zůstat, jak se argument blíží k a.

Všimněte si, že jsme tak zodpověděli jednu z otázek v úvodu. Jmenovitě, jestliže jsme blízko k a, pak se hodnoty f dají aproximovat určitým číslem, jmenovitě tou limitou, a hra nám dokonce dovoluje být přesní, pokud je to třeba: Je-li dána tolerance, vím, jak blízko k a zůstat, aby byla aproximace dostatečně přesná. Teď jsme připraveni na definici.

Hovorové názvy: "f jde k L pro x jdoucí k a", "f jde k L v a", "f má limitu L v a". Podrobněji o zápise pojednává tato poznámka.

Definice specifikuje slovo "limita" coby výsledek limitní otázky (to číslo L), pokud existuje. Lidé ale také toto slovo používají k označení samotné otázky, obzvláště je-li vyjádřena značením "lim( f )". Je tedy například možné se zeptat, "jakého typu je limita lim_x→a( f )", i když ani nemusí být zřejmé, jestli má tato otázka rozumnou odpověď (tj. zda existuje příslušné L podle definice). Pokud takové L existuje, pak se mu dle definice říká limita. Může to znít směšně, že "limita" (číslo) je výsledkem "limity" (příkladu), ale tahle neopatrnost zřídkakdy působí problémy. Teď když tomu rozumíme, se můžeme vrátit k definici.

Jestliže má funkce takovou limitu (číslo jako v definici) v daném bodě, pak limita  lim_x→a( f )  (příklad) se nazývá konvergentní, nebo také řekneme, že tato limita konverguje. Jinak se (limitní příklad) nazývá divergentní, nebo řekneme, že ta limita diverguje.

Všimněte si, že nerovnost "0 < |x − a|" odebírá bod a samotný z relevantní množiny, nekontrolujeme, jestli příslušná hodnota leží v pruhu, přesně jak už jsme inzerovali. Klikněte si sem, pokud chcete vidět úplný a korektní důkaz podle definice, že ta limita v úplně prvním příkladě je správně.

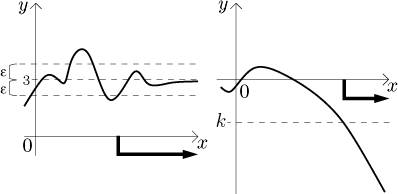
Měli jsme dva příklady na limitu, která funguje. Je užitečné podívat se také, co se může pokazit. Uvažujme následující tři situace.

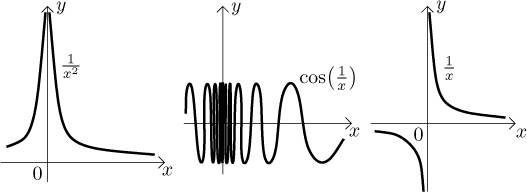
Co se dá říct o limitě v nule? U prvního grafu (toho vlevo) nemůžeme mít limitu, protože ať už zkusíme jakékoliv číslo L, funkce od něj vždy uteče hned vedle a = 0, takže není naděje, že bychom se toho vybouchnutí dokázali zbavit odříznutím kusů grafu trochu dále od a.

V druhém grafu máme funkci, která nevybouchne (tedy přinejmenším ne kolem a), ale neustále osciluje mezi 1 a −1. Ať zůstaneme jakkoliv blízko k a, vždy tam bude další velká oscilace. Tohle chce možná trošku více detailů: Čísla 1/(kπ) jdou k 0. To znamená, že kdykoliv zvolíme nějaké δ > 0, jedno z těchto čísel bude v intervalu (0,δ), takže také to další číslo, 1/([k + 1]π), tam bude. Ale funkce cos(1/x) je rovna 1 v jednom z nich a −1 v druhém (které je které záleží na paritě k), což dokazuje, že ať už zkusíme jakékoliv δ > 0, stejně bude vždycky oscilace mezi −1 a 1 do vzdálenosti δ od a = 0.

Proto také neexistuje L, který by fungovalo jako limita. Schválně si zkuste nějaké takové vybrat. Když nám někdo dá malé epsilon, jmenovitě menší než 1, pak odpovídající vodorovný pruh okolo L bude mít šířku menší než 2, takže z něj oscilace velikosti 2 vyskočí, ať už je ten pruh kdekoliv, tj. ať už jste zvolili jakékoliv L. A protože - jak jsme viděli v předchozím odstavci - jsou tyto oscilace libovolně blízko k a, nemůže existovat delta, které by přinutilo funkci, aby zůstala v pruhu. Všimněte si, že zde bylo zásadní, že velikost oscilace zůstává velká. V sekci sin(1/x) v části Teorie - Elementární funkce jsou nějaké variace tohoto příkladu, jedna z nich také neustále osciluje, ale velikost oscilace se zmenšuje až k nule a limita tam funguje.

Třetí graf je v určitém smyslu kombinací výbuchu a pohybu ve dvou různých směrech, jak se blížíme k a zleva a zprava, některé hodnoty uletí nahoru (napravo) a jiné dolů (nalevo).

I když existuje mnoho totálně šílených funkcí, první dva grafy jsou ve skutečnosti typickými příklady, co se může pokazit. Kdykoliv máme divergentní limitu, je tam buď nějaký výbuch, nebo oscilace, která se nechce uklidnit, nebo kombinace obojího.

Je zde ale ta druhá otázka: Když se začneme přibližovat k a, co se stane s f? Z tohoto úhlu pohledu teď vidíme mezi těmi třemi divergentními příklady rozdíl. V prvním grafu nemáme konvergenci, ale pořád můžeme dodat užitečnou informaci, jmenovitě: Když se x blíží k 0, pak se funkce zvětší nad libovolnou mez, neboli jde to nekonečna. V dalších dvou příkladech nelze říct nic určitého, protože jak se blížíme k 0, tak buď funkce žádnou tendenci nemá (druhý graf), nebo jich má víc najednou. To nás přivádí k jinému pohledu na limitu, budeme muset udělat další definici. V předchozí definici jsme hovořili o vlastní limitě, reálném čísle. Teď představíme nevlastní limity, nekonečno a mínus nekonečno. V definici se pokusíme zachytit ideu, že f roste nad všechny možné meze. Zase použijeme formát hry. Tentokráte, abychom dostali nekonečno jako limitu, nám někdo navrhne mez a my musíme ukázat, že blízko a se funkce nad tuto mez dostane a také tam zůstane.

Symetrická situace dá mínus nekonečno coby limitu.

Definice.
Uvažujme funkci f definovanou na nějakém prstencovém okolí bodu a. Řekneme, že ∞ je limita funkce f pro x jdoucí k a, nebo že funkce jde do nekonečna pro x jdoucí k a, jestliže pro každé reálné číslo K existuje nějaké δ > 0 tak, aby pro všechna x∈D( f ) splňující 0 < |x − a| < δ platilo f (x) > K.

Řekneme, že −∞ je limita funkce f pro x jdoucí k a, nebo že funkce jde do mínus nekonečna pro x jdoucí k a, jestliže pro každé reálné číslo k existuje nějaké δ > 0 tak, aby pro všechna x∈D( f ) splňující 0 < |x − a| < δ platilo f (x) < k.
Značení pro limitu rovnou nekonečnu je

Značení pro limitu rovnou mínus nekonečnu je

Píšeme také "f →∞ pro x→a" v prvním a "f → −∞ pro x→a" v druhém případě.

Jak vidíte, je to zase hra, tentokráte si protivník vybírá (při limitě nekonečno) velice velká K, aby nám to ztížil; pokud jde o mínus nekonečno, protivník by typicky zvolil za k velká záporná čísla, aby funkci vytlačil dolů.

Teď si v tom potřebujeme udělat pořádek, protože máme dva druhy limity. Jestliže máme limitu podle první definice, reálné číslo, nazývá se vlastní limita a máme konvergenci. Jinak je to divergence. Existují dva druhy divergence. Ten pěknější je, že máme pořád ještě limitu, buď nekonečno nebo mínus nekonečno. Tyto se jmenují nevlastní limity. Pokud máme limitu, ať už vlastní nebo nevlastní, řekneme, že limita existuje. Ten "špatný" druh divergence je, že neexistuje ani nevlastní limita, což se stává, když se do toho zamíchá nějaká oscilace. Pak prostě řekneme, že limita neexistuje, a píšeme

Abychom to shrnuli, konvergence je o aproximaci funkcí čísly. Pokud je to možné, máme vlastní limitu a konvergenci, jinak máme divergenci. Existence limity je dána otázkou "co se stane s f, když se přiblížíme k a". Buď nějaká odpověď je (funkce jde k jistému číslu, do nekonečna, do mínus nekonečna), pak limita existuje, nebo nelze říct něco určitého a limita neexistuje.

Důležitá poznámka: Když jsme psali definici vlastní limity, chtěli jsme, aby funkce zůstala do vzdálenosti ε od L, neboli vlastně jsme chtěli, aby f zůstalo v ε-okolí bodu L, označovaném U_ε(L). Teď jsme chtěli, aby f zůstalo v intervalech (K,∞) v prvním a (−∞,k) v druhém případě. Jaká to náhoda, toto jsou přesně typická okolí pro ∞ a −∞. V první definici jsme to měli těžší, když byla okolí malá, tj. když bylo epsilon malé. Abychom udělali okolí nekonečna malým, chceme, aby bylo K velké. Připomeňme, jak vypadá definice ε-okolí nekonečna: U_ε(∞) = (1/ε,∞). Všimněte si, že když pošleme epsilon do nuly (zprava, od kladných čísel), pak 1/ε poroste nad všechny meze, neboli děláme ta okolí "malá". Podobně to funguje i pro mínus nekonečno. To ukazuje, že i pro nevlastní limity můžeme použít epsilon-okolí a podstata hry se nezmění.

Všimněte si, že ty dvě definice - pro vlastní a nevlastní limitu - se lišily v jediném místě: Specifikaci toho, co vlastně chceme od funkce f. Teď se ukazuje, že tyto dvě rozdílné specifikace lze napsat jedním společným způsobem pomocí U_ε(L), kde L teď může být i nekonečno či mínus nekonečno. Tyto dvě zdánlivě rozdílné definice lze tedy napsat jako jednu pomocí okolí, protože i tu delta-podmínku lze vyjádřit pomocí prstencových okolí.

Než to ale uděláme, uvedeme další dva druhy limity, které se pak také zapíší pomocí tohoto obecného způsobu.

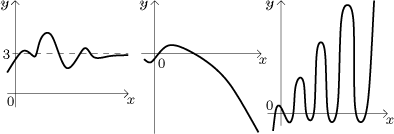
V situaci prvního grafu bychom mohli říct, že když je x opravdu velké, tak jsou funkční hodnoty přibližně 3. Tomu říkáme limita v nekonečnu, je to limita vlastní a konvergence. Další dva případy jsou divergence. V druhém grafu nemůžeme funkci aproximovat nějakým číslem, ale pořád se dá něco říct. Máme tam nevlastní limitu, jmenovitě mínus nekonečno. Třetí případ je ten "špatný", kdy není žádná limita, je to typická kombinace výbuchu a oscilace. Všimněte si, že tam není limita nekonečno, protože ačkoliv funkce roste výše a výše nad všechny meze, tak tam nakonec nezůstane, což nesouhlasí s tím, jak cítíme limitu.

Abychom napsali pořádně definici limity v nekonečnu, musíme se rozhodnout, jak hrát hru. Víme, jak specifikovat požadavek, u vlastní limity bychom chtěli, aby (po odříznutí nechtěných částí funkce) zůstaly hodnoty f v pruhu daném nějakým epsilon, pro limitu nekonečno/mínus nekonečno bychom chtěli, aby funkce (tedy zase jen její kousek) zůstana nad/pod nějakou danou mezí. Víme už také, že oba tyto požadavky jde spojit do jediného vyjádření pomocí epsilon-okolí. Jak vyjádříme to odřezávání? Chceme říct, že "pro dané okolí limity (vlastní či nevlastní, teď umíme obojí) zůstane funkce nakonec v tomto okolí, tj. když zůstaneme dostatečně daleko vpravo". Ale zůstat na pravém konci se dá zase přeložit do jazyka okolí nekonečna, tentokráte nekonečna na ose x.

Je samozřejmě možné se také zeptat na limitu v mínus nekonečnu, pokud tam tedy funkce jde. Podobně jako u limity v a, abychom se mohli ptát na limitu v nekonečnu/mínus nekonečnu, potřebujeme, aby byla funkce definovaná na nějakém prstencovém okolí.

Teď jsme připraveni na obecnou definici.

Definice (limita - obecná definice).
Nechť f je funkce, nechť a je reálné číslo, ∞ nebo −∞. Předpokládejme, že f je definovaná na nějakém prstencovém okolí bodu a. Nechť L je reálné číslo, ∞ nebo −∞. Řekneme, že L je limita funkce f pro x jdoucí k a, jestliže pro každé ε > 0 existuje nějaké δ > 0 tak, aby pro všechna x∈D( f ) splňující x∈U_δ(a) − {a} platilo f (x)∈U_ε(L).

Pokud najdeme limitu L, která je reálné číslo, řekneme, že je to vlastní limita a že limita (ten příklad) konverguje. Jinak řekneme, že limita (ten příklad) diverguje.
Limita nekonečno nebo mínus nekonečno se nazývá nevlastní limita. Pokud najdeme nějakou limitu (vlastní či nevlastní), řekneme, že limita existuje. Jinak řekneme, že limita neexistuje (neex).

Pro limitu teď máme čtyři možnosti. Můžeme hledat limitu ve vlastním bodě (nějaké reálné a) a pokud ji najdeme, může být vlastní či nevlastní. Můžeme také hledat limitu v nevlastním bodě (v nekonečnu či mínus nekonečnu) a zase, pokud ji najdeme, může být vlastní nebo nevlastní.

Zde se můžete podívat na důkaz podle definice, že 2x − 1 jde v nekonečnu do nekonečna.

Abyste se ujistili, že máte pro limitu správný cit, podívejte se na následující dva grafy a zkuste uhádnout jejich limity v mínus nekonečnu, −2, 0, 2 a nekonečnu, pak se podívejte, jestli vám to vyšlo stejně jako nám.

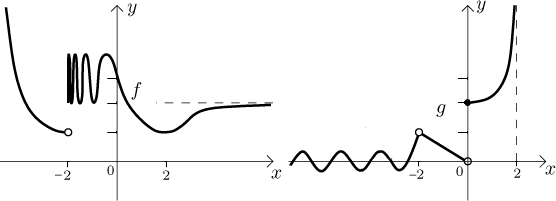
Odpovědi:

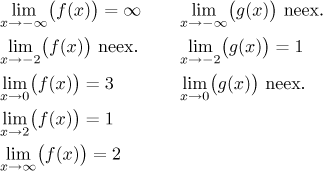
Limitu g v bodě 2 a v nekonečnu jsme neodpovídali, protože otázka nemá smysl, funkce není definována na žádném prstencovém okolí bodu 2 a také není definovaná na žádném okolí nekonečna. Když totiž řekneme, že "limita neexistuje", pak to znamená, že otázka má smysl (funkce je defiovaná na nějakém prstencovém okolí toho konkrétního a), jen prostě nemáme pěknou odpověď. Situace s g okolo 2 je jiná, tam nemá smysl ani otázka. Všimněte si také, že máme limitu g v −2, i když ta funkce tam není definovaná; to už by nemělo překvapit, víme, že hodnota g v bodě −2 nemá žádný vliv na limitu v −2 a ani nemusí existovat.

Předpoklad, že f existuje na nějakém prstencovém okolí a, může být občas zrádný. Uvažujme například tangens okolo nekonečna. Na první pohled by se zdálo, že tam tangens dojde, takže se můžeme podívat na jeho limitu v nekonečnu; nicméně body, kde tangens neexistuje, jdou do nekonečna, takže ať už vezmeme jakékoliv okolí nekonečna (na ose x), vždy v něm budou body, kde tangens není definován. Nemůžeme se tedy zeptat na limitu v nekonečnu.

Když jsme nahoře mluvili o limitě v a, zdůrazňovali jsme, že se k a blížíme z obou stran. Někdy ale pomůže, kdybychom se k a blížili jen z jedné strany. Například u posledního obrázku neměla funkce f limitu v −2, ale když se blížíme k a = −2 pouze zleva, rozhodně vidíme nějakou tendenci. Můžeme se k −2 blížit také zprava, ale tam máme nepříjemnou oscilaci a žádnou limitu. Přirozeně tak přicházíme k pojmu jednostranné limity, limity v a zleva a limity v a zprava.

Poznamenejme několik věcí. Za prvé, abychom měli jednostrannou limitu, nepotřebujeme vlastně funkci na druhé straně a. Můžeme tedy použít jednostranné limity v situacích, kdy máme funkci jen na nějakém jednostranném prstencovém okolí bodu a. Například pro tu funkci g v obrázku nahoře se můžeme zeptat na limitu v bodě 2 zleva (existuje na nějakém levém prstencovém okolí bodu 2), i když jsme se nemohli zeptat na limitu v 2.

Za druhé, protože se jednostranné limity dívají na menší část funkce, máme větší šanci, že dostaneme rozumnou odpověď. Často tedy používáme jednostranné limity v situaci, kdy ve skutečnosti chceme znát obyčejnou (oboustrannou) limitu, ale situace je obtížně zvládnutelná a může pomoci, když se podíváme jen na jednu stranu.

Za třetí, máme teď tři druhy limity. Ten původní pojem a teď i limitu zleva a limitu zprava. Když řekneme limita, vždy míníme tu původní, oboustrannou, o které jsme mluvili výše. Když někdy mluvíme o více druzích limity najednou, zdůrazníme ten původní pojem slovy "oboustranná limita".

Konečně, všimněte si, že jednostranné limity mají smysl pouze u vlastních bodů a. Limita v nekonečnu je totiž zároveň limitou zleva, limita v mínus nekonečnu je zároveň limitou zprava. Proto v nevlastních bodech nemluvíme o jednostranných limitách.

Teď uděláme příslušné definice.

Definice (jednostranné limity).
Nechť f je funkce, nechť a je reálné číslo takové, že f existuje na (a,a  +  b) pro nějaké b > 0. Nechť L je reálné číslo, ∞ nebo −∞. Řekneme, že L je limita funkce f pro x jdoucí k a zprava, jestliže pro každé ε > 0 existuje nějaké δ > 0, δ < b tak, aby pro všechna x∈(a,a + δ) platilo f (x)∈U_ε(L).

Nechť f je funkce, nechť a je reálné číslo takové, že f existuje na (a − b,a) pro nějaké b > 0. Nechť L je reálné číslo, ∞ nebo −∞. Řekneme, že L je limita funkce f pro x jdoucí k a zleva, jestliže pro každé ε > 0 existuje nějaké δ > 0, δ < b tak, aby pro všechna x∈(a − δ,a) platilo f (x)∈U_ε(L).

Poznámka: Podmínka δ < b ve hře zaručuje, že (a,a + δ) je podmnožinou (a,a + b), popř. že (a − δ,a) je podmnožinou (a − b,a), takže funkce existuje na takových pravých a levých prstencových delta-okolích.

Značení pro limitu zprava:

Můžeme také psát "f →L pro x→a⁺", v krátkosti dokonce píšeme "f (a⁺) = L".

Značení pro limitu zleva:

Můžeme také psát "f →L pro x→a^-", v krátkosti dokonce píšeme "f (a^-) = L".

Vraťme se k těm dvěma grafům nahoře. Zkuste uhádnout všechny možné jednostranné limity a pak je porovnejte se správnými odpověďmi.

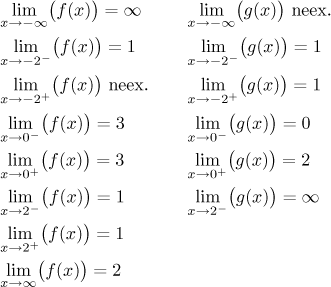
Pro g teď máme limitu v bodě 2 zleva, ale pořád tam není limita zprava.

Jednostranné limity mají vlastnosti velice podobné limitě. Většina vět, které platí pro limity, také platí pro jednostranné limity, jak také uvidíme v následujících sekcích. Zde uvedeme větu, která spojuje tyto dva pojmy. Všimněte si, že definice jednostranné limity vyžaduje méně než definice limity, odkud plyne, že když je L limita f v a, pak je to automaticky i limita v a zleva a limita v a zprava. Opačný směr vyžaduje existenci a rovnost.

Věta.
Nechť f je funkce definovaná na nějakém prstencovém okolí reálného čísla a. Nechť L je reálné číslo, ∞ nebo −∞. Pak L je limita funkce f v bodě a tehdy a jen tehdy, jestliže je L také limita f v a zleva a zprava.

Podmínku lze vyjádřit krátkým zápisem takto: lim_x→a( f ) = L právě tehdy, pokud f (a⁺) = f (a^-) = L.

Důležitá poznámka: Všimněte si, že pojem limity je lokální pojem. To znamená, že výsledek závisí pouze na tom, co se stane hned vedle limitního bodu, chování f dále od a je zcela irelevantní. (Pro úplnost připomeňme, že také hodnota f v a je irelevantní.) Můžeme to vyjádřit takto:

Nechť f a g jsou dvě funkce, uvažujme bod a. Jestliže existuje prstencové okolí bodu a, jakkoliv malé, na kterém f = g, pak se limity f a g v a rovnají.

Toto je občas docela užitečné, můžeme opatrně nahradit nepříjemnou funkci nějakou lepší, pokud jsou stejné na nějakém prstencovém okolí. Analogická tvrzení také samozřejmě platí pro jednostranné limity a jednostranná okolí.

Tuto sekci uzavřeme větou, která není zrovna dvakrát užitečná, ale ukazuje, že pojem limity je rozumný:

Věta.
Jestliže má funkce limitu (oboustrannou, jednostrannou) v nějaké bodě a, pak je tato limita jednoznačně určena.

Jinými slovy, není možné mít v jednom bodě dvě různé limity.

Základní vlastnosti, výpočet limity
Zpět na Teorie - Limita