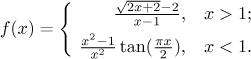
Problem: Evaluate (if it exists) the limit at x = 1 of the function
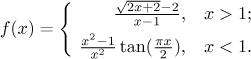
Solution: Here we have a two-sided limit, but the function is not defined by one expression on some reduced neighborhood of the limit point. However, it is given by one formula on each side, so we pass to one-sided limits.
Limit at 1 from the right: The function is given on a right reduced neighborhood of 1 by the first formula, the one with square root, so we start by substituting 1 into this formula and get "zero over zero", an indeterminate ratio. In that box we have two possible methods for this particular expression. One is the l'Hospital rule.
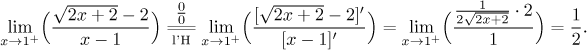
As expected, differentiation did not get rid of the root, but fortunately it cleared out the rest so we got the answer. The other approach, which is usually better (but not here), is to get rid of the roots using the algebraic trick from the box "difference of roots".
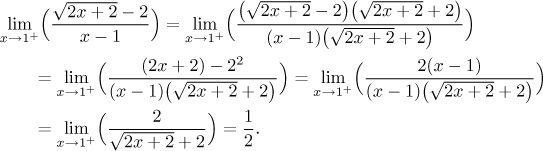
Either way, we now have
Limit at 1 from the left: The function is given on a left reduced neighborhood of 1 by the second formula, the one with tangent, so we start by substituting 1 into this formula.
![]()
This is an indeterminate product and the standard procedure is this: We change this product into a fraction and then apply l'Hospital's rule. An experienced limiteer can already see that this way it will be unpleasant.

Is there a better way? Sure, isolate the source of trouble (parts that give infinity) and do the "nice" part separately.

Either way, we now have
Since the limit at 1 from the right is different from the limit at 1 from the left, the conclusion is that the limit of f at 1 does not exist.