Probably the most popular misconception concerning limits at infinity is this: When trying to find a limit of a rational function (ratio of polynomials), it helps to cancel the smaller of the dominant terms.
Now this "rule" is not completely wrong. In fact, when the dominant terms in the numerator and the denominator are equal, then cancelling is the shortest way to find the limit.
Example:
![]()
Here x2 is the dominant term both in the numerator and the denominator, so we can find the limit by cancelling x2 (that is, we divide both the numerator and the denominator by it).
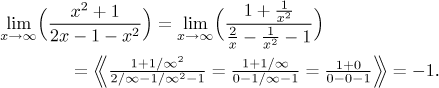
Short and sweet, wasn't it? Check that solving this problem by factoring out of dominant terms is actually the same procedure, just a bit longer to write.
With a bit of luck, the "cancel smaller dominant" rule also helps in other problems:
Example:
![]()
Here x2 is the dominant term in the numerator and x4 is the dominant term in the denominator. We will try to cancel x2, the smaller of them:
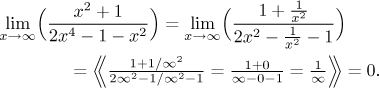
We were lucky and got the answer. Why are we talking about luck? Just a little change in the problem will cause this method to fail:
Example:
![]()
We still have x2 as the dominant term in the numerator and x4 as the dominant term in the denominator, so we try to cancel x2:
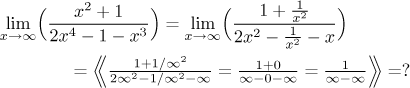
We see that the method "cancel the smaller of the dominant terms" failed, it lead to an indeterminate form.
However, the method of factoring out still works:
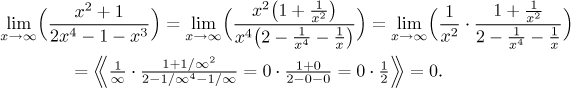
Perhaps this example would make you think that we should be cancelling the larger of the two dominant terms, since in this example cancelling x4 actually helps:
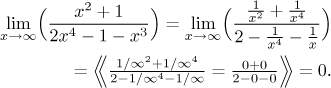
Unfortunately, this also cannot be taken as a general rule, because it fails in many cases.
Example:
![]()
Now x4 is the dominant term in the numerator and x2 is the dominant term in the denominator. What happens if we try to cancel the larger one, x4?
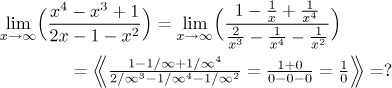
The expression
You can check by factoring out that
What is the point we are trying to make? The method of factoring out that we recommended is reliable. If the two dominant terms are equal, then cancelling also works, and it is a bit easier to write. When the dominant terms are not equal, then cancelling the smaller one or cancelling the larger one may sometimes help, but it also often fails. Experience should suggest when cancelling is advisable, but when you are not sure, factoring out dominant terms and putting them together is always the safe way.
By the way, this applies not only to rational functions, that is, ratios of polynomials, but also to ratios of sums of "other expressions" like 2x, factorial etc.