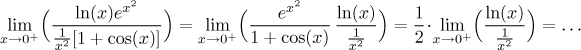
One of the favourite tricks is to split a given limit into several parts and evaluate each of them separately. It is especially useful when we have a limit with a "nice" part and a more difficult part, we then prefer to do the nice part right away, like this:
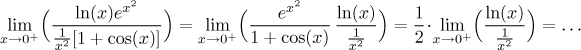
This problem should be solved using the l'Hospital rule and it is definitely easier to do it in the simplified situation.
Now look at this example:
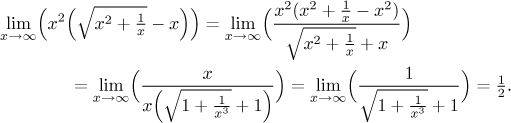
It might be tempting to try a similar simplifying trick. For instance, the
part
![]()
It definitely was easier, but it was obviously wrong. Why in the first example the "partial substitution" was correct, while in the second example it wasn't?
In fact, it is never correct to substitute to just a part of the expression in the limit. If we do want to evaluate just a part, we have to try to make it into a separate limit using theorems on limit and operations. In the first example we would go like this:
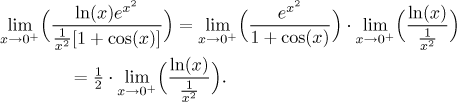
Now we can substitute in the first limit, since there we substitute into the whole expression in that particular limit. What happens in the second example? We will try the same, we have to break the limit into lots of smaller ones so that one of them only has the 1/x in it:
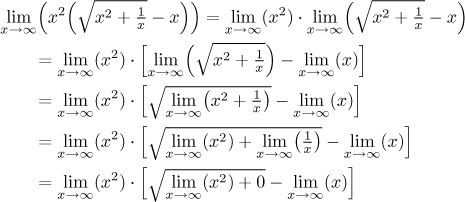
This seems to work, so where is the difference? In what comes the next.
Recall that the equalities in theorems on limit and operations are
"conditional"; that is, we do not know that the limit can be split that way
until we get to the end of all calculations and they make sense. What do we
know about the first example? There we ended with half of some limit. No
matter what the answer will be for that second limit, when we multiply this
answer by a half, we always get something meaningful. In other words, there
is no indeterminate product featuring
In the other example the situation is very different, since we cannot guarantee that there would be no indeterminate expressions. In fact there will be:
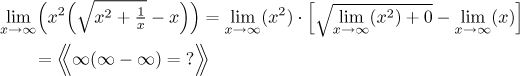
This distinction is at the core of the matter. If we want to evaluate just a part of the given expression in the limit, we have to first isolate it into a limit of its own. Then we have to work out the rest and watch out for indeterminate expressions. Sometimes we see right away that there will be no indeterminate expression coming. The most typical cases are these (assume that f has a proper limit A at a):
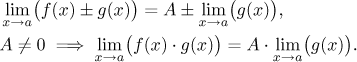
Why is it so? The only indeterminate expression in addition/subtraction is the difference of infinities, which cannot happen when we know that A is proper. Concerning the product, the indeterminate expression is zero times infinity. We can therefore do the splitting for sure if we know that this situation cannot happen, that is, if A is not infinity nor zero.
We conclude this note with one last example. Recall that for any real number c we have
![]()
Therefore it would be wrong to do "partial substitution" like this:
![]()
Where is the catch?
![]()
and