Derivative and operations

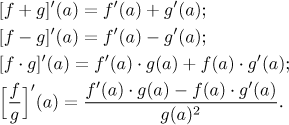
Algebraic approach to derivatives requires two components. The first is elementary derivatives, which are the basic building blocks from which we will construct derivatives. The second ingredient is grammar, rules by which we put together the elementary derivatives. In other words, we need to know how to differentiate a function that is created by combining elementary functions using algebraic operations and composition. First we will look at local statements.

Theorem.
Assume that functions f and g are both differentiable at a. Then the functions f  + g, f  − g, and f ⋅g are differentiable at a, and the function f /g is differentiable at a if g(a) ≠ 0. Moreover, the derivatives satisfy

Example:

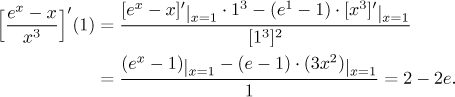
Theorem.
Assume that a function f is differentiable at a and a function g is differentiable at b = f (a). Then the composed function g ○ f = g( f ) is differentiable at a and

Note that we substitute b into g′, which is logical. When you picture how the functions act, you will see that a lives in a space different from the one where g has its domain, so it cannot be substituted into g.

Example:

Theorem.
Assume that functions f and g are both differentiable on an open set G. Then the functions f  + g, f  − g, and f ⋅g are differentiable on G, and the function f /g is differentiable on G assuming that g ≠ 0 on G. Moreover, the derivatives satisfy

Example:

Theorem (The chain rule).
Assume that a function f is differentiable on an open set G and a function g is differentiable on the set f [G]. Then the composed function g ○ f = g( f ) is differentiable on G and

Example:

We will return to this example below.

The proper use of these formulas is explained in Methods Survey. Here we will investigate these rules closer. We start with a simple corollary.

Theorem (derivative is linear).
Assume that functions f and g are both differentiable on an open set G and A, B are real numbers. Then

[Af  + Bg]′ = Af ′ + Bg′.

This theorem is very important if we want to consider differentiation as a transformation from one space of functions (namely, all functions differentiable on a certain set G form a linear space) into another space of functions. Since transformations that are linear are the "best" transformations, it is nice to know that differentiation satisfies this condition.

The chain rule

Here we will look closer at the chain rule. We will try to present it in different ways, since it is usually the most difficult part of differentiation for students, on the other hand it is really quite simple, it is just a matter of understanding it. If it seems difficult when exposed the usual way, perhaps you will see it better in a different way.

We start by observing that the chain rule actually tells us what happens to a derivative of a function when we change its variable via substitution. For simplicity we will assume that all functions we mention here are differentiable wherever we need it.

Consider a function g that depends on a variable y. We can differentiate it, obtaining g′(y). What happens if we introduce a new variable via substitution y = f (x)? We get a new function h(x) = g( f (x)). What is the derivative of this new function? Of course, if we have a formula for this function, we can simply calculate a concrete derivative, but often we need a general formula that relates h ′ to g′. The chain rule says that

h ′(x) = g′(y)⋅f ′(x) = g′( f (x))⋅f ′(x).

We can rewrite this as follows:

Fact.
If the variable y depends on another variable x, then

[g(y)]′ = g′(y)⋅y′.

To see how it works we return to the last example above, where we wanted to calculate the derivative of sin(2x). This is a composed function. When we denote y = 2x, we obtain sin(y), which is not a composed function any more, it is an elementary function whose derivative we remember. Thus using the above rule

[sin(2x)]′ = [sin(y)]′ = cos(y)⋅y′ = cos(2x)⋅[2x]′ = 2cos(2x).

In fact, one can think of this as a general rule, and indeed there are textbooks where they do not have elementary derivatives as we had them in the previous section, but their list has entries like

[y^a]′ = ay^a−1⋅y′,       [e^y]′ = e^y⋅y′,       [sin(y)]′ = cos(y)⋅y′ etc.

Such a rule works also for "ordinary" functions, since if y is the basic variable, then y′ = 1 and we get [y ^a]′ = ay ^a−1 etc. as usual. These formulas are therefore generalizations of "our" formulas, they work both with the basic variable and with transformed variable.

Another interesting point of view at the chain rule is to look at this substitution business via the Leibniz notation. The rule then reads

It seems as if the chain rule was just cancelling in fractions, since we get the left hand side by cancelling dy on the right. This is just another advantage of pretending that the differentials exist (cf. Leibniz notation). When I learned calculus informally in high school, it was explained to us via differentials by our physics teacher (we needed it to solve problems) and it all seemed natural. I used to cancel d's left and right and it never failed me. Then I started to study math seriously and I learned that it was wrong :-).

One last remark. Why is it called the chain rule? The next section shows the reason.

How do the above rules work if more functions are involved? Linearity is a rule that readily adopts to more summands even for general transformations, so it must also work for differentiation:

[A₁ f ₁ + A₂ f ₂ + ... + A_n f _n]′ = A₁ f ₁′ + A₂ f ₂′ + ... + A_n f _n′.

We also have a rule for the product of more functions. We first show a formula for three functions to show the basic idea and then the general rule:

[ f ⋅g⋅h]′ =  f ′⋅g⋅h  +  f ⋅g′⋅h  +  f ⋅g⋅h′

[ f ₁⋅ f ₂⋅...⋅ f _n]′ =  f ₁′⋅ f ₂⋅...⋅ f _n +  f ₁⋅ f ₂′⋅...⋅ f _n + . . . +  f ₁⋅ f ₂⋅...⋅ f _n′

Note that it is not necessary to remember these rules, because they can be easily deduced from the rules for two functions. Indeed, addition and multiplication are associative operations, so we can insert parentheses at suitable places to change the expression into an addition/multiplication of two terms and use the usual rule. Rather then complicated explanations we prefer to show an example, where we deduce the rule for the product of three functions.

[ f ⋅g⋅h]′ = [ f ⋅(g⋅h)]′ =  f ′⋅(g⋅h)  +  f ⋅[g⋅h]′
=  f ′⋅(g⋅h)  +  f ⋅(g′⋅h + g⋅h′) =  f ′⋅g⋅h  +  f ⋅g′⋅h  +  f ⋅g⋅h′.

Similarly, it is not necessary to remember the rule for composition of more functions. Again, we prefer to show a simpler version for three functions, since the notation for a general case is quite complicated (too many compositions and functions). If you understand the idea, you easily find the derivative of a hundred composed functions.

[h(g( f ))]′ = h′(g( f )) ⋅g′( f )⋅ f ′.

As you can see, when we have a chain of composed functions as in the picture,

we differentiate the one at the end (the one that is done last) and substitute into it whatever was there before. Then we disregard the outer function we just differentiated and apply the same procedure to its inside part and again and again...

Example:

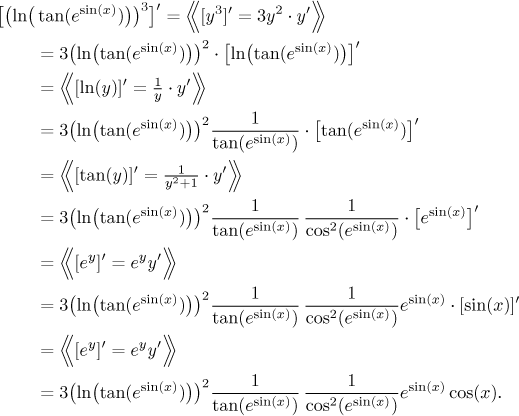
Now you see why it is called the chain rule. By the way, an experienced "differentiator" (or "derivator" as in Terminator) would skip all the steps and go right to the answer, creating it term by term.

By the way, since division is not an associative operation, there is no rule for "more ratios". For starters, what does it mean "more ratios"? Since there is no obvious answer to this, it is clear that we cannot get any rule here.

Again, linearity makes it simple to iterate differentiation. For the k^th derivative we get

[Af  + Bg]^(k) = Af ^(k) + Bg^(k).

For a product things get a bit more interesting, iteration of the product rule leads to the Leibniz formula

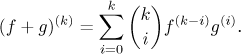
For instance, [ f  + g]′′ = f ′′g + 2 f ′g′ + f g′′. Does it look familiar? Well it should! Here's the famous binomial formula for the k^th power:

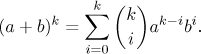
An amazing coincidence, isn't it? There are no rules for higher order derivatives of other operations.

Although finding an inverse function (if it exists at all) is not an operation per se, differentiation is very nice and allows us to find the derivative of the inverse function using the derivative of the original function.

Theorem.
Assume that f is a function that is continuous and strictly monotonee on some neighborhood of a point a. If f is differentiable at a and f ′(a) ≠ 0, then its inverse f ₋₁ is differentiable at b = f (a) and

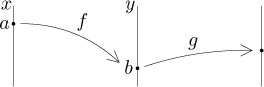
Note that a functions that is strictly monotone is automatically invertible. To understand why we substitute what we substitute, we look at a picture of the situation:

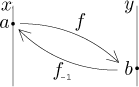
Obviously, b is the right place to differentiate the inverse function, since it cannot accept a which lives in a different world. On the other hand, the only reasonable candidate to put into f ′ is a. How would the formula look as a rule?

Things get even more interesting if we rewrite this rule using the Leibniz notation. We have y = f (x) and also x = f ⁻¹(y). Thus the inverse function rule reads

Now isn't that nice? To show how this rule can be applied we derive the formula for the derivative of logarithm. We know that y = ln(x) is the inverse function to e ^y.

Back to Theory - Derivative