Funkce dané rozpisem (či funkce definované po částech) se objevují docela často, například jediný rozumný způsob, jak zkoumat funkce s absolutní hodnototu, je zbavit se jí rozdělením výrazu na dva případy (či více, pokud tam je absolutních hodnot více). Jak s takovými funkcemi pracujeme?
Základní pravidlo je následující: Každý výraz, který definuje danou funkci na určité množině M, zkoumáme obvyklým způsobem, ale pak musíme omezit naše závěry na onu množinu M. Když toto uděláme se všemi výrazy a množinami, "dáme vzniklé obrázky vedle sebe" a dostaneme obrázek celé funkce. Zase máme dva základní přístupy. Dá se dělat zvlášť kompletní analýza každého výrazu a na konci spojit výsledky. Druhý způsob je kombinovat informace o definujících výrazech v každém kroku. Ukážeme oba přístupy. Vynecháme detaily, pro další informace o jednotlivých krocích viz příslušné sekce v části Přehled metod - Průběh funkce.
Příklad: Načrtněte průběh funkce
Řešení: Definičním oborem je celá reálná osa, funkce je tam spojitá. Než půjdeme dál, zbavíme se absolutní hodnoty.
![]()
Jak už jsme psali, máme teď dvě možné strategie.
1. Nakreslíme každý vzorec zvlášť.
To je něco, co ve skutečnosti dělám zřídka, ale u tohoto příkladu je to
snadné.
První výraz dává vzhůru orientovanou parabolu. Nejlépe její tvar určíme,
když najdeme její kořeny a vrchol. Pro kořeny máme kvadratický vzorec,
dostaneme
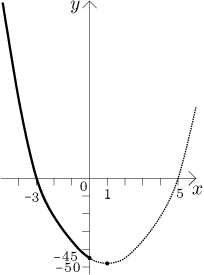
Druhý výraz je kubická křivka. Určíme ji nalezením kořenů a dvou "ohybů".
Když zkusíme dosazovat malá celá čísla, brzy uhodneme, že
Tento kvadratický výraz nemá kořeny, takže tato kubická křivka jde přes osu x pouze v jednom bodě.
Abychom našli "zatáčky", podíváme se po lokálních extrémech vyřešením
rovnice
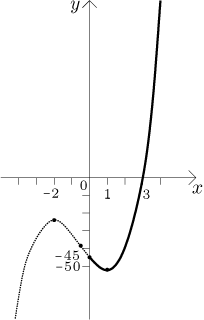
Teď dáme obrázky dohromady a dostaneme graf funkce f. Aby byl opravdu
dobrý, měli bychom udělat ještě jednu věc: Podíváme se na jednostranné
derivace v 0. Dostaneme
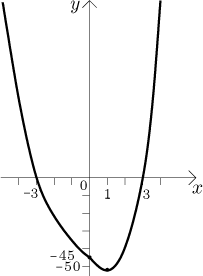
Důležité vlastnosti f (monotonie, konvexita) teď odvodíme z vlastností oněch dvou křivek pomocí selského rozumu.
2. Integrace dat krok za krokem.
Tento přístup funguje tak, že děláme všechny kroky najednou pro všechny
výrazy z definice funkce. V každém kroku rovnou ignorujeme informace, které
sice vyšly z určitého výrazu, ale nejsou relevantní pro f, protože
neleží v oblasti, kde dotyčný výraz souhlasí s f. Bývá dobrý nápad
takový proces strukturovat, aby si člověk připomněl, že vždy musíme
porovnávat výsledky s oblastmi platnosti. Já si obvykle rozdělím reálnou osu
na oblasti a udělám odpovídající sloupce, ve kterých pracuji, v každém
sloupci používám jen výraz ze záhlaví a vyškrtávám všechny výsledky, které
leží mimo dotyčný sloupec.
Abychom tento postup ukázali, vrátíme se k Příkladu. Tam jsme některé kroky dělali snadno v původní formě s absolutní hodnotou. Abychom si ten spojovací postup ukázali v plné obecnosti, budeme ignorovat daný tvar a předstírat, že už je funkce dána od začátku rozpisem:
![]()
Začneme definičním oborem. Každý výraz existuje na množině, kde dává f, a tyto množiny se spojí a dají celou reálnou osu, takže to bude definiční obor. Výrazy pro kladnou a zápornou půlku nevypadají podobně, takže máme podezření, že tato funkce není symetrická. Toto podezření potvrdíme tak, že zkusíme dosadit dva symetrické body:
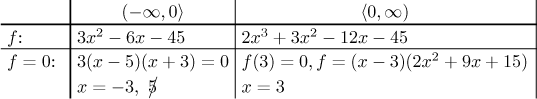
Všimněte si, že jsme vyškrtli kořen 5, protože nepatří do té části reálné
osy, kde pracujeme; jinými slovy, v bodě
Teď se podíváme na limity v koncových bodech intervalů definičního oboru a z definice, zase v každém bodě použijeme příslušné vzorce.
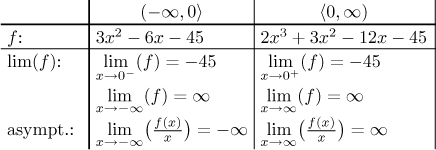
Protože také
Další krok je najít derivaci a určit monotonii.
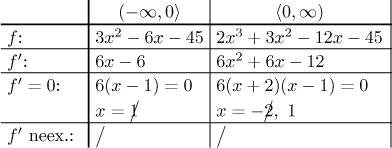
Máme jeden kritický bod,

Ten řádek s
Zpět k tabulce. Vidíme dva sousedící intervaly se stejnou monotonií, dají se
spojit? Protože je funkce f spojitá v 0, tak rozhodně dají. Závěr tedy
je, že f je klesající na
Poslední krok je najít druhou derivaci a určit konvexitu.
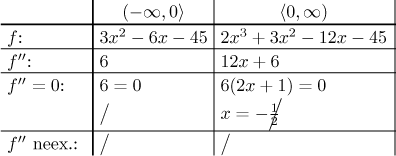
Nejsou žádné dělící body (kromě automatického

Funkce f je proto konvexní na
Standardní kroky jsou hotovy, zde se ještě také podíváme na jednostranné
derivace v 0, abychom správně nakreslili to napojení. Dostaneme
Nejprve zvolíme měřítko. Protože máme hodnoty jen z rozmezí −3 až 3, dáme rozsah mezi −5 a 5 (abychom měli trochu místa k práci) na ose x. Hodnoty zde kolísají od 0 (průnik s osou x) po −52. Abychom to tam všechno zmáčkli, rozhodli jsme se zmenšit osu y desetkrát v porovnání s osou x.
Pak tam zakreslíme všechny body, které se v jednotlivých krocích objevily,
jmenovitě

Může pomoci, když zkombinujeme ty dvě tabulky, než kreslíme graf.
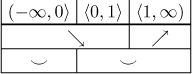
Pro další příklady viz tento příklad s funkcí danou rozpisem a tento příklad s absolutní hodnotou v Řešených příkladech - Průběh funkce.