Zde použijeme fyziku, abychom zkusili pochopit, proč by mohla být základní věta integrálního počtu pravdivá.

Nechť f (t) je funkce definovaná na ⟨a,b⟩. Použijeme následující interpretaci:

Představte si, že řídíte auto po dálnici a v čase t = a minete kilometrovník s číslem "000". Jedete dál a zapisujete si okamžitou rychlost na tachometru jako funkci f (t), až po čas t = b. Jaká je vaše pozice F(x) v čase t = x měřená podle kilometrovníků? Více podrobností o této situaci najdete v této poznámce v sekci Úvod k reálným funkcím, je ale třeba upozornit, že abychom tento příklad dobře připodobnili základní větě, museli jsme přejmenovat funkce. Pozice, kterou zde značíme F, se v oné poznámce značí r.

Když jedete t hodin konstantní rychlostí v, urazíte d = vt kilometrů. Toho ale nemůžeme v našem případě použít, protože rychlost se stále mění. Protože jde o situaci ze života, dá se předpokládat, že funkce f je "pěkná". To znamená, že pokud se v nějakém čase t podíváme na opravdu kraťoučký časový interval dt, rychlost se téměř nemění. Můžeme tedy změnu polohy ds během časového intervalu dt spočítat jako f (t) krát dt. Celková změna polohy (uražená dráha) se dostane sečtením malých změn během všech krátkých intervalů dt mezi t = a a t = x:

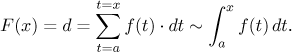
Teď také vidíme, proč jsme nemohli použít proměnnou x jako integrační proměnné, když už ji máme jako mez integrálu. Když jedno takové x zvolíme, potřebujeme ještě pořád možnost se pohybovat v čase během sčítání malých příspěvků rychlosti, takže potřebujeme ještě jednu proměnnou.

Každopádně jsme právě viděli, že pozice F(x) je dána tímto integrálem. Protože z fyziky víme, že derivace pozice dává rychlost, dostaneme F ′ = f a F je tedy primitivní funkcí k f, přesně jak tvrdila Základní věta č. 1

Teď si představme, že v čase t = a není na kilometrovníku "000", ale nějaké jiné číslo. Zase použijeme F k záznamu pozice měřené pomocí kilometrovníků, například F(a) udává naši pozici na začátku. Z fyziky víme, že F je primitivní funkce rychlosti f. Dráhu (ujetou vzdálenost) mezi časy t = a a t = b lze spočítat pomocí poziční funkce F, ale také sečtením příspěvků rychlostí, jak jsme to již jednou dělali. Tak dostameme

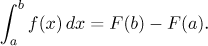
To je přesně Newton-Leibnizova formule.

Tato nerovnost je někdy zapisována takto:

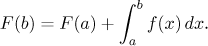
V naší interpretaci to znamená následující: Abychom našli naši pozici v čase b, začneme s pozicí v čase a a přičteme všechny změny odpovídající naší okamžité rychlosti mezi časy a a b.
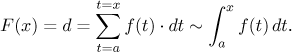
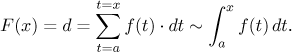