Theorem.
Let f be a Riemann integrable function on
![]()
and
![]()
are true.
Here we will look at some properties of the Riemann integral that are not directly related to its evaluation, but are more of a theoretical interest.
Theorem.
Let f be a Riemann integrable function on[a,b]. Then the equalities
and
are true.
Note that the integrals in limits make sense. Consider the first equality: We
assume that f is Riemann integrable on
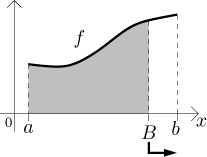
If we cut away a part of the region along the right edge and make this cut-away part smaller and smaller, the resulting areas should converge to the whole area.
Similarly, f is Riemann integrable on
The second property we will cover here is a modification of the standard Mean Value Theorem (see Derivatives - Theory - MVT) for the function F defined in the Fundamental Theorem of Calculus:
![]()
The Fundamental theorem then says
![]()
When we substitute for F, we get the following thorem.
Theorem (The Mean Value Theorem for integrals, Lagrange theorem for integrals).
Let f be a continuous function on[a,b]. Then there is a number c in(a,b) such that
If we recall the definition of an average of f (see Applications - Average), we can restate the Mean Value Theorem as follows:
Theorem.
Let f be a continuous function on[a,b]. Then there is a number c in(a,b) such thatf (c) is equal to the average of f over the interval[a,b].
Note that the continuity in the assumption of the Mean Value Theorem is
crucial. Indeed, recall the example of a jump function we saw before. Its average over
The Mean Value Theorem for integrals has many versions. The one we stated above is probably the most popular, but also the weakest, merely a reformulation of the good old MVT. There are much stronger statements, we will show one of the more popular here.
Theorem (The Mean Value Theorem for integrals).
Let f be a continuous function on[a,b] and g an integrable function on[a,b] that is positive there. Then there is a number c in(a,b) such that
Note that if you use this theorem with the constant function