The standard method of evaluating a definite integral is based on the
Fundamental theorem of calculus:
First one finds an antiderivative F of the given function f on
the given interval
![]()
Obviously, the crucial step here is to be able to find the antiderivative. What to do in case this fails is beyond the scope of Math Tutor.
Beware: The Newton-Leibniz formula only works for functions f that
are continuous on the closed interval
While the Newton-Leibniz formula is usually reliable, there are two situations when one might want to do the evaluation differently. Namely, when finding and antiderivative involves substitution or integration by parts, then it is possible (and shorter) to evaluate the definite integral right away.
If we want to use substitution in a definite integral, we simply transform the limits of integration using the basic substitution formula:
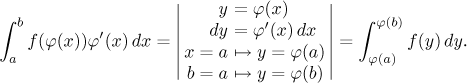
For more details and an example see Substitution in Theory - Methods of Integration.
If we want to use integration by parts in a definite integral, we apply the limits of integration to both parts of the new expression in the natural way:
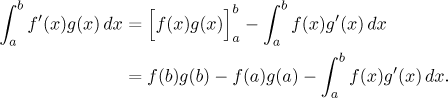
That is, we substitute limits into the part of the antiderivative that is already done. See also Integration by parts in Theory - Methods of integration or this example in Solved Problems - Integration.