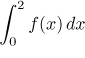 , where
, where
Example: Evaluate
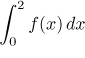 , where
, where
![]()
Solution: This function looks like this:
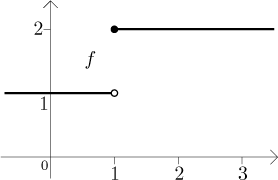
We have to decide on partitions. Note that in rectangles that do not involve
the point
![]()
We look at the picture
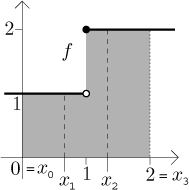
and see that
![]()
Thus
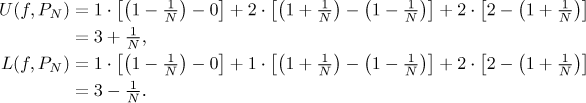
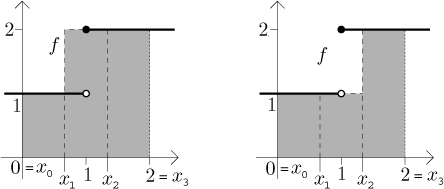
The upper and lower sum can be also directly seen from the picture, the shaded area on the left is the upper sum, on the right the lower sum:
We therefore get bounds for infimum and supremum
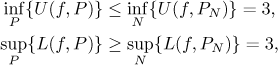
and so
![]()
Consequently,
![]()
and
![]()
This answer seems clear from the picture, the region consists of three squares of side one.