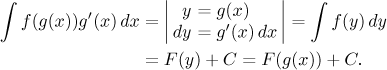
Substituce

Substituce je nejmocnější a zároveň asi nejjednodušší metoda na výpočet integrálů, proto se ji většinou snažíme použít. Nevýhodou je, že funguje jen někdy. Je tedy nutné se naučit nejen metodu samotnou, ale praxí také získat schopnost odhadnout, kdy je substituce výhodná. Obecná myšlenka substituce je popsána v této poznámce.

Přímá substituce

je založena na této matematické větě. V ideálním případě by se dala vyjádřit tímto postupem:

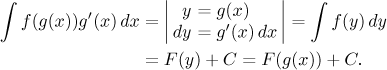
Takže si zvolíme transformaci y = g(x) a doslova nahradíme všechny výskyty funkce g(x) symbolem y. Potřebujeme také nahradit dx. K tomu slouží odvozená rovnost v druhém řádku, podle ní pak výraz g′(x)dx nahrazujeme symbolem dy.

Pokud se substituce povede, dostáváme nový integrál, který při troše štěstí dokážeme vyřešit. Pak je ještě třeba provést tzv. zpětnou substituci, tedy přejít zpět k původní proměnné, to je ale snadné, máme na to vzorec.

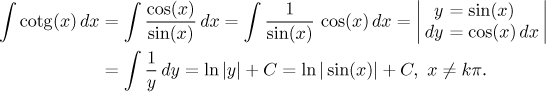
Jak to ladí s formální větou o substituci? Máme funkci f (y) = e^y a zajímá nás integrál, ve kterém je f složena s g(x) = sin(x). Tento komplikovanější integrál nás zajímá na intervalu J všech reálných čísel, protože vždy hledáme integrál na co největší množině a zde není důvod se nějak omezovat. Funkce g tento interval zobrazí na interval I = ⟨−1,1⟩. Podle věty o přímé substituci stačí umět najít neurčitý integrál funkce f na intervalu I, což je ta střední pasáž ve výpočtu výše. Pak do výsledku dosadíme g a dostaneme odpověď na původní otázku, a to na původním intervalu I.

Krása onoho zápisu výše je, že nás zbavuje všech těchto úvah, neřešíme J a I, prostě chceme vyměnit jeden vzorec za jiný. Nemusíme také myslet na to, že by se podle věty v tom komplikovaném integrálu kromě složeného f měla vyskytovat také derivace funkce g. Substituční postup nás totiž nutí dosadit nikoliv za dx, ale za g′(x)dx. Pokud by to tam nebylo (tedy pokud by v integrálu nebyl také ten kosinus), tak tato substituce neprojde. Při praktickém výpočtu se tedy lidé větou nějak neabývají, onen postup předvedený výše zaručí, že je vše v pořádku.

Hlavní slabinou je, že u dx musíme mít g′(x) a x se musí vyskytovat zásadně ve formě g(x), jinak by zvolená substituce s g nebyla možná. To se ale povede málokdy. Naštěstí se substituci dá pomoci, díky čemuž se z ní stává jeden z nejmocnějších nástrojů. Jak to funguje?

Základní požadavek je, že z integrálu po substituci musí původní proměnná zcela zmizet. Jediným nástrojem je zvolená transformace y = g(x) a odvozená rovnost dy = g′(x)dx, je nám ale povoleno také tyto rovnosti upravovat algebraicky tak, abychom získali vzorce, které nám umožní nahradit výrazy s x pomocí výrazů s y. Tím získáváme ohromnou svobodu, je ovšem nutno mít na paměti, že pak už nepoužíváme přesně matematickou větu o přímé substituci, takže výsledek nemusí být vždy správně. Je tedy opravdu dobré udělat zkoušku derivací výsledku (což se ostatně u integrálů doporučuje vždy), ale popravdě řečeno, problémy vznikají jen při opravdu divokých úpravách, většinou to v pohodě projde. Ukážeme si teď jednu aplikaci tohoto obecnějšího přístupu.

Lineární substituce.
Myslíme tím libovolnou substituci ve tvaru y = Ax + B, která vede na rovnost dy = A⋅dx. Zde se není třeba spoléhat na to, že se A⋅dx objeví v integrálu, protože můžeme tuto rovnost vždy přepsat jako dx = (1/A)dy a pak v integrálu nahradit dx. Ukážeme si to na jednom docela důležitém příkladě.

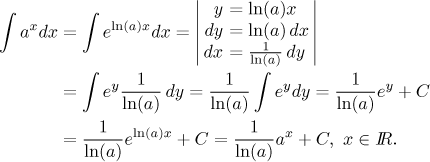
Integrál je samozřejmě platný jen pro a > 0, aby byla obecná exponenciála definovaná. Mnoho lidí považuje tento integrál za tabulkový a učí se jej nazpaměť.

je založena na této matematické větě. V ideálním případě by se dala vyjádřit tímto postupem:

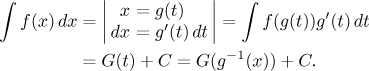
Vypadá to, jako bychom jen následovali přímou substituci výše v opačném směru, a něco na tom je. Tam jsme se snažili zjednodušit integrál tím, že jsme si (složitý) výraz nahradili jedním písmenkem, zde naopak děláme integrál složitějším, ale základní mechanismus zůstává: Zvolíme si transformaci a pak ji použijeme k přeměně integrálu, také rovnost pro nahrazení diferenciálu dostáváme tak, že zderivujeme g a použijeme to jako koeficient. Nicméně uvnitř jde o rozdílný proces, což se odráží například v tom, že zde jsou nároky na g vyšší (například musí být na rozdíl od přímé substituce invertibilní).

Je zde také rozdíl v obtížnosti fází. Přímá substituce má problém hned na začátku, hlavně s nahrazením dx, což často zvolenou substituci znemožní, ale zpětná substituce je jasná. Naopak u nepřímé substituce není při jejím provádění s dx problém, z x = g(t) přímo dostáváme dx = g′t)dt, zato zpětná substituce může být docela dobrodružná, zvlášť pokud se chceme dostat k příjemným výsledkům.

Proč by vlastně chtěl někdo udělat integrál komplikovanějším, než už je? Nikterak překvapivě se nepřímá substituce používá velice zřídka, ale jsou jisté typy integrálů, u kterých pomůže, a zkušení integrátoři vědí, že se pak určité nepřímé substituce nakonec magicky zjednoduší (viz integrály s odmocninou v Přehledu metod - Integrace). Ukažme si jednoduchý příklad tohoto typu.

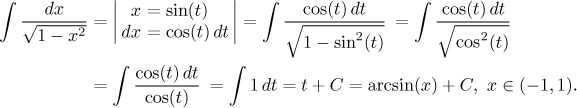
Popravdě řečeno jde o tabulkový integrál a měli byste si jej pamatovat.

Poznamenejme, že i tento snadný integrál je již sdostatek dobrý, aby ukázal, že nepřímá substituce zas není tak snadná, jak vypadá. Pečlivý čtenář se měl zarazit u prvního integrálu v druhém řádku: Neměla by tam ve jmenovateli být absolutní hodnota? To je velice dobrá otázka a odpověď závisí na tom, jak vlastně tuto nepřímou substituci děláme. Podle věty bychom měli vzít funkci g = sin(t), která jde z nějakého intervalu J do našeho intervalu (−1,1). Tento interval J musí být zvolen tak, aby na něm byla g prostá a aby obraz J vzhledem k g dával celý interval (−1,1). Nejpřirozenější volba je interval , takže nový integrál po substituci je uvažován na tomto intervalu. Tam je kosinus vždy kladný, takže opravdu nemusíme používat absolutní hodnotu, když ve jmenovateli rušíme navzájem druhou odmocninu a druhou mocninu. Všimněte si ale, že pokud si zvolíme jiný interval J, tak se může stát, že už budeme muset absolutní hodnotu použít. Jak vidíme, je to další rozdíl, u přímé substituce se o intervaly starat nemusíme.

je vlastně kombinace přímé i nepřímé substituce a používá se jí hlavně ke zkrácení výpočtu v případech, kdy by bylo nutno použít několika substitucí v řadě. Zkušení integrátoři si tak dokážou ušetřit spoustu času. Začíná transformací h(y) = g(x) a druhou důležitou rovnost dostaneme obvyklým způsobem, na obou stranách zderivujeme a přidáme diferenciály: h′(y)dy = g′(x)dx. Uvedeme si jeden příklad, který lze také spočítat aplikováním dvou jednodušších substitucí za sebou (zkuste si to, je to dobrý trénink):

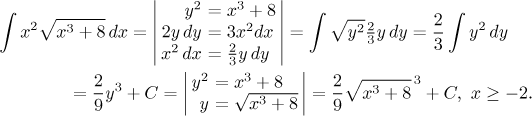
I zde je potřeba být opatrný, na jakém intervalu nová proměnná žije, u tohoto příkladu je třeba se rozhodnou mezi intervaly ⟨0,∞) a (−∞,0⟩, protože y² má být na pracovním intervalu prostá. Ve výsledku to nebude hrát roli, ale může to silně ovlivnit průběh výpočtu, jak ostatně také uvidíme níže.

Je to v zásadě stejné jako substituce v integrálu neurčitém. Psali jsme, že základní pravidlo substituce je změnit vše z jazyka x do jazyka y, což zahrnuje také meze. Jak se změní? Jako obvykle, pomocí naší základní transformace y = g(x). Příklad:

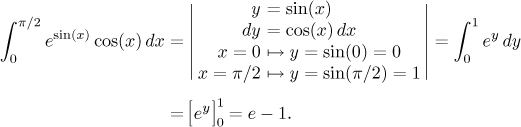
Podobně měníme meze u substituce nepřímé a smíšené, ale tam je to poněkud obtížnější. Například výše jsme měli smíšenou substituci y² = x³ + 8. Kdyby šlo o integrál určitý a jedna z mezí byla x = 2, tak bychom ji dosadili do transformační ronvice a pak hledali odpovídající y. Zde jsou dvě volby, plus a mínus 4, ta správná záleží na volbě intervalu J při substituci.

Pro praktické návody a příklady se podívejte na sekci Substituce v části Přehled metod - Metody integrace.

Další sekce: per partes
Zpět na Teorie - Metody integrace