Příklad: Vypočítejte integrál
![]()
Řešení: Tento integrál patří do šuplíku "podíl lineár", použijeme tedy příslušný postup, jmenovitě substituce. Měli bychom si označit ten podíl písmenem y, ale abychom se zbavili odmocniny, použijeme triku s nepřímou substitucí a označíme si podíl výrazem y2:
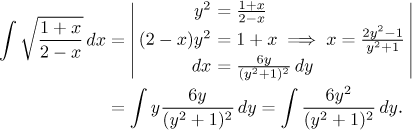
Dle očekávání máme parciální zlomky, budou dva se čtyřmi konstantami. Protože nemáme lineární kořeny, nezískáme nic zadarmo. Obecná metoda je roznásobovací, někdy se hodí pomocné metody ke zkrácení výpočtu, ale tady je už ta roznásobovací docela jednoduchá. Detaily jsou zde. Dostaneme
![]()
První integrál je tabulkový, na druhý nasadíme redukční vzorec:
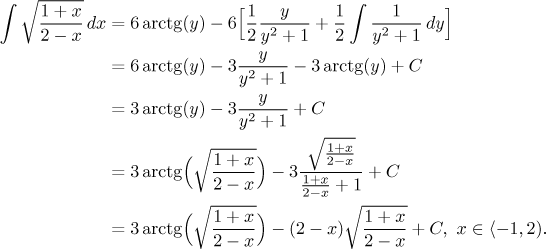
Integrační obor je dán intervalem, na kterém je výraz pod odmocninou nezáporný, navíc nesmí být nula ve jmenovateli (ale může být v čitateli). Vzhledem k použití nepřímé substituce je zkouška naprostou nutností.
Co můžeme dělat, když si nepamatujeme ten redukční vzorec? Pro druhou
mocninu existuje zajímavá alternativa, jmenovitě podívat se na to jako na
integrál ze šuplíku
integrály s mocninami kvadrátů.
Pro tento kvadrát se doporučuje substituce s
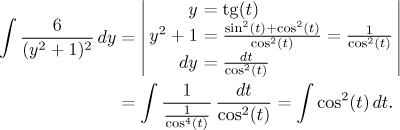
Dostali jsme klasický integrál, který se snadno řeší pomocí identity.
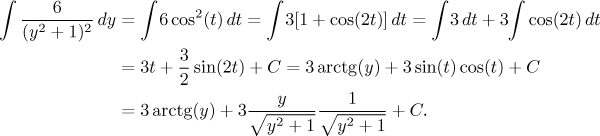
Je to stejný vzorec, jaký jsme dostali z redukčního vzorce. Jako obvykle nebyla zpětná substituce zrovna snadná a příslušné vzorce k nahrazení sinu a kosinu jsme našli pomocí vhodného trojúhelníka. Poznamenejme, že kdyby byla mocnina ve jmenovateli vyšší, pak by byl nový goniometrický integrál dost těžší.
U tohoto příkladu existuje ještě jedna zajímavá alternativa, která nám umožní integrovat přímo původní racionální lomenou funkci. Vychází z postřehu, že bychom uměli substitucí integrovat takto:
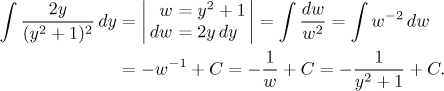
V porovnání s tímto má náš původní integrál (před rozkladem na parciální zlomky) bohužel v čitateli jedno y navíc, ale my víme, jak se extra mocnin zbavit: metodou per partes. Podmínkou je, abychom uměli integrovat to, co zbyde, ale to jsme právě provedli. Můžeme tedy psát:
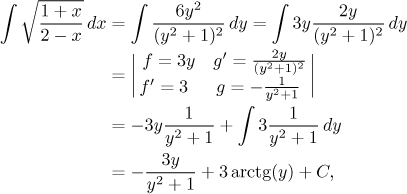
což je přesně ten výsledek, který jsme předtím dostali redukcí.