Příklad: Vypočítejte integrál

Řešení: Nejprve si spočítáme neurčitý integrál. V tomto integrálu není žádný "extra sinus" nebo "extra kosinus", aby nám umožnil snadnou substituci, výraz ve jmenovateli se nám také nepodaří zjednodušit, takže se musíme podívat hlouběji do šuplíku "goniometrické integrály". Naštěstí nemusíme použít univerzální substituce, protože se v našem integrálu vyskytují jen sudé mocniny goniometrických funkcí. Je tedy možno použít tangensovou substituci:

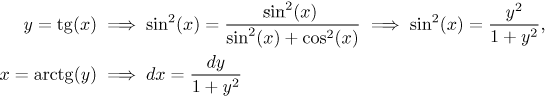
V tomto okamžiku se ovšem musíme omezit na nějaký interval , kde k je zvolené celé číslo. Tato volba se neprojeví algebraicky na výpočtu, výsledek bude ale platit pouze na tomto zvoleném intervalu. Teď trochu předbíháme, ale všimněte si, že žádný takovýto interval nebude stačit na náš integrační interval ⟨0,2⟩. To nám na konci příkladu poněkud zkomplikuje život.
Zatím nás to ale ještě netrápí a počítáme:

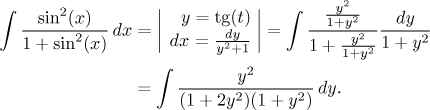
O dalším postupu není pochyb, jde o integrál z racionální lomené funkce. Nasadíme proto parciální zlomky, vzniknou dva s nerozložitelným kvadrátem ve jmenovateli. To znamená, že nedostaneme žádné konstanty zadarmo zakrývacím trikem, takže je třeba najít čtyři rovnice. Lze vyzkoušet spolehlivou násobící metodu a vyjde docela pěkně, takže snad ani nestojí za to zkoumat alternativy, ale kdo chce, může potřebné čtyři rovnice získat pomocí lmitní a dosazovací metody. Detaily rozkladu jsou zde. Dostaneme

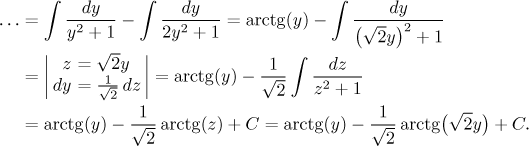
Nyní je čas na zpětnou substituci. V druhém členu prostě dosadíme za y, protože tento výraz již nejde zjednodušit. Zajímavější je to u prvního členu, kde se sejde tangens s arkustankensem. Zde je důležité si uvědomit, že vlastně integrujeme na intervalu , takže dostaneme

Tato (pevně zvolená) konstanta k je pak spolknuta integrační konstantou C, takže můžeme psát:

To je samozřejmě pěkný výsledek, ale má podstatnou vadu. Protože integrujeme funkci, která je všude spojitá (všimněte si, že jmenovatel je vždy nejméně jedna), měla by existovat primitivní funkce na celé reálné ose. Bohužel jsme ji nebyli schopni najít, což je obzvláště smutné proto, že teď bychom potřebovali primitivní funkci na intervalu ⟨0,2⟩, ale žádný z intervalů, na kterých jsme mohli počítat, jej nepokrývá.

Velice často se stane, že když se podíváme na výsledný algebraický vzorec

tak zkouškou zjistíme, že platí pro celý definiční obor integrálu. V našem případě tomu tak ale bohužel není, protože bod (ani jeho posuny o kπ) nejdou do výsledku dosadit. (Nicméně se přesvědčte, že v ostatních bodech reálné osy je opravdu derivace F ′ rovna integrované funkci.)

To je vážný problém. Normálně bychom situace, kde máme primitivními funkc jen na podintervaly, řešili příslušným rozdělením integrálu. Na to ale potřebujeme mít primitivní funkce na uzavřených intervalech, zatímco zde je máme jen na intervalech otevřených, přesně řečeno vadí, že není pokryt bod . Jsou dva rozumné způsoby, jak se s tím vyrovnat. Jedna je, že se daný integrál považuje za nevlastní integrál. Výpočet pak jde následovně.

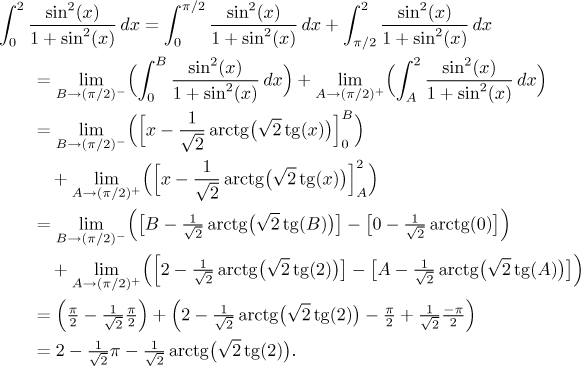
Druhou alternativou je zkusit vyrobit primitivní funkci na celém zadaném intervalu spojením částečných výsledků. Nejprve prozkoumáme F okolo kritického bodu . Jednostranné limity jsou

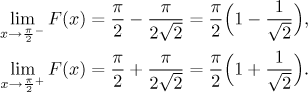
Jde zde tedy o skokovou nespojitost. Situace vypadá takto:

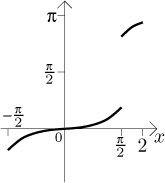
Vlastně jde o dobrou zprávu. Mohli bychom zkusit najít primitivní funkci tak, že bychom vzali funkci F na intervalu a v bodě k ní "přilepili" další kopii funkce F, ale posunutou dolů o konstantu tak, aby na sebe navazovaly. Definujeme tedy:

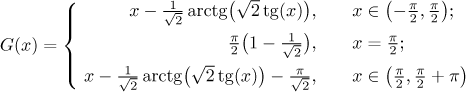
Přesvědčte se, že tato G je opravdu spojitá v bodě . Díky tomu, že na intervalu je G jen posunem funkce F, je tam G primitivní funkcí, totéž samozřejmě platí na intervalu . Teď ještě potřebujeme dokázat, že

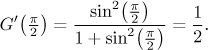
Podle definice by to bylo dost drsné, proto raději použijeme matematickou větu. Protože G je spojitá v (ověřte si to, proto jsme to tak slepovali) a protože žádaný derivační vztah platí na prstencovém okolí bodu , pak musí derivace odpovídat i v bodě . Tento závěr se dokáže pomocí jednostranných limit G ′ v tomto kritickém bodě, přesně jak jsme to dělali u předchozího příkladu.

Můžeme tedy říct, že G je hledaná primitivní funkce na intervalu, který rovněž zahrnuje integrační interval. Můžeme proto psát:

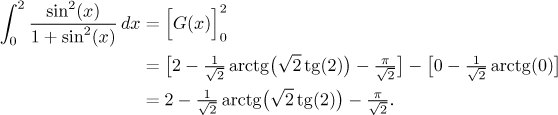
Zde se dočtete, jak by se hledala primitivní funkce na celé reálné ose.

Zpět na Řešené příklady - Integrace