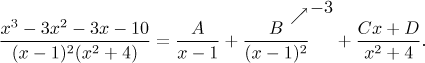
Zde ukážeme několik metod, které lze použít k určení neznámých konstant v rozkladu na parciální zlomky. Budeme je ilustrovat na rozkladu
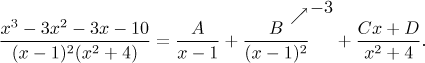
Jednu konstantu jsme již určili zakrývací metodou, protože ta je nejjednodušší a nemá smysl hledat k ní alternativu. Ostatní konstanty bychom standardně určili násobící metodou, což je přesně chvíle, kdybychom ocenili nějakou alternativu.
Lineární faktory 1.
Začneme s problémem nalezení A, obecně s hledáním konstant u
lineárních faktorů, které se objevují ve vyšší mocnině. První zajímavá
metoda je založena na selském rozumu. Pomocí zakrývací metody určíme

Takže jsme A našli, ale úprava podílu nalevo dala asi víc práce než celá násobící metoda. Mohou ale být příklady, kte toto pomůže.
Lineární faktory 2.
Zde se pokusíme zobecnít zakrávací metodu. Připomeňme, že je založena na
následujícím postupu. Vezmeme rozklad, který se soustředí na nějaký lineární
faktor
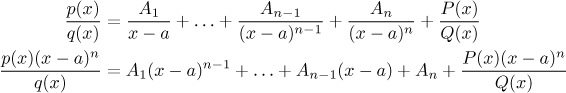
Pak jsme dosadili
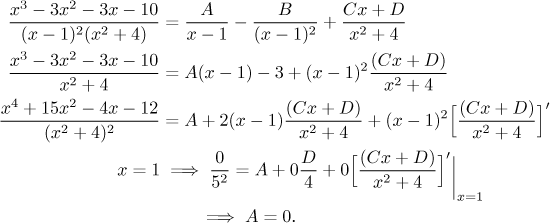
Osobně bych raději dělal násobící metodu. Pokud derivujeme vícekrát, dostaneme také další konstanty. To je zajímavé z teoretického hlediska, protože dostáváme obecný vzorec pro všechny konstanty u zlomků s lineárami. (Pokročilí čtenáři mohou vidět zajímavou souvislost s rezidui a obecně Laurentovým rozvojem komplexních funkcí.)
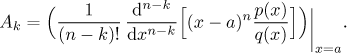
Kvadratické faktory 1.
Zde je možné použít zajímavou verzi dosazovacího triku. Konstanty u
lineárních faktorů (u nejvyšších mocnin) lze získat dosazovaním kořenů
lineár, u konstant z kvadratických parciálních zlomků nejvyšších mocnin
zase zabere dosazení komplexního kořene.
U našeho příkladu má komplexní faktor kořen
![]()
Porovnáním reálné a imaginární části získáme rovnice
V případě, že by jeden kvadratický člen byl přítomen vícekrát, získáme zase pouze koeficienty u nejvyšší mocniny.
Kvadratické faktory 2.
Pokud vám nevadí komplexní výpočty, nabízí se ještě jeden trik.
Pokud povolíme komplexní kořeny, tak lze každou ryzí racionální funkci
rozložit na parciální zlomky založené na lineárních členech neboli na těch
nejpříjemnějších. Vzniknou pak i komplexní koeficienty. V našem příkladě
dostaneme
![]()
Teď můžeme použít zakrývací trik s příslušnými kořeny a dostaneme b, c a d, u posledních dvou to bude
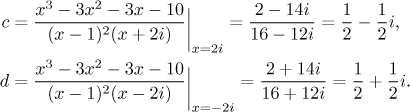
Poslední konstantu
![]()
Získali jsme tak rozklad, jehož další výhodou je, že nemá kvadratické členy, takže jej vlastně integrujeme zpaměti:
![]()
Nevýhody jsou dvě. Museli jsme provádět dost hnusné komplexní výpočty, což možná některým nebude až tak vadit. Větším problémem je, že výsledek integrace obsahuje komplexní čísla, jenže zadaná funkce je reálná. Výsledek by tedy měl být rovněž reálný, takže se získaný komplexní výsledek integrace ještě musí upravovat do reálného tvaru, což nemusí být jednoduché (a většinou rozhodně není). Snad z toho důvodu se tento trik s komplexním rozkladem nepoužívá pro integraci v reálném oboru.