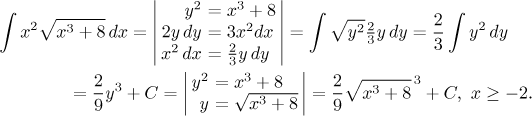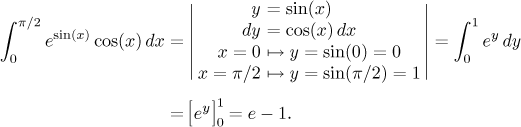Substitution
Substitution is the most powerful and at the same time perhaps the easiest
method of evaluating integrals, which is why it is our method of choice. It
has one disadvantage: sometimes it fails. Therefore we not only need to learn
the mechanics of substitution itself, but also acquire some feeling for when
the substitution works and when it fails. This comes with experience.
The general idea of sustitution (not just in integral) is described in
this note.
Direct substitution
is based on this mathematical
theorem. In the ideal case it can
be expressed by this procedure:
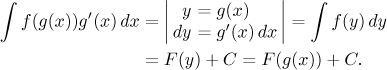
That is, we choose a transformation
y = g(x) and use it to literally
replace all appearances of g(x) with the symbol
y. We also need to replace dx. For this we use the equality we
deduced in the second row, according to it we replace
g′(x)dx with dy.
If this substitution succeeds, we obtain a new integral and with a bit of
luck we can solve it. Then one has to also do a so-called back
substitution, that is, return back to the original variable, but that is
simple, we have a formula for it.
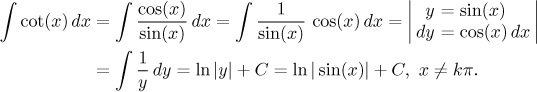
How does this tie in with the formal theorem on substitution? We have a
function
f (y) = ey
and we are interested in in an integral that features f composed with
g(x) = sin(x). This more
complicated integral is considered on the interval J of all real
numbers, since we always want the integral on the largest possible set and
there is no reason to restrict ourselves to something smaller. The function
g maps this interval onto the interval
I = [−1,1]. According to the theorem on direct
substitution, it is enough to find an indefinite integral of the function
f on the interval I, which is the middle part in the
calculation above. Into the formula that we obtained we substitute g
and get the answer to our original question, valid on the original
interval I.
The beauty of the procedure we use above above is that it allows us to
dispose of all this theoretical reasoning, we do not worry about J
and I, we simply want to exchange one expression for another.
We also need not remember that according to that theorem we also need to
have the derivative of g in that complicated integral with composed
f. The substituting procedure forces us to replace not dx but
g′(x)dx. If we do not find it there
(that is, if we did not have that cosine in the integral), then this
substitution can't be done. Thus when doing practical calculations people
do not worry about that theorem, the procedure we have shown above
guarantees that everything is fine.
The main weakness is that we need to have that
g′(x) next to dx and that x
must appear exclusively in the form of g(x),
otherwise the chosen substitution with g would not be possible.
However, this is rarely possible. Fortunately, one can help it, which makes
substitution one of the most powerful tools. How does it work?
The basic requirement is that after the substitution, all
x must disappear from the integral. The only tool available is the
chosen transformation y = g(x)
and the related equality
y = g′(x)dx, but
we are also allowed to change these equalities algebraically in order to
obtain formulas that allow us to replace expressions featuring x with
expressions featuring y. This gives us tremendous freedom, but one
should remember that in such a case we do not use the quoted theorem as
stated, so then we are on a shaky ground and the answer may come out wrong.
It is therefore strongly recommended to check that our result is correct (by
differentiating it) - actually, we should do this with every integral we
solve. Actually, there is rarely any trouble unless you get really wild with
those formulas. We will now show one example of this more general approach.
Linear substitution.
By this we mean any substitution of the form
y = Ax + B, which
leads to the equality
dy = A⋅dx. Here we do not
have to rely on the expression
A⋅dx appearing in the integral, since we can
always rearrange this equality to
dx = (1/A)dy and then replace
dx in the integral. This means that we can always do any linear
substitution. We will show one fairly important example.
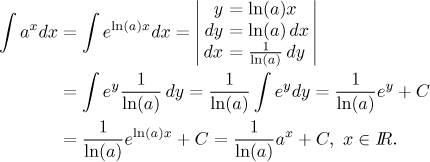
The integral is of course only valid for
a > 0, otherwise the generalized exponential
does not exist. Many people consider this integral an elementary one and
memorize it.
Indirect substitution
is based on the following mathematical
theorem. In the ideal case it can
be expressed by this procedure:
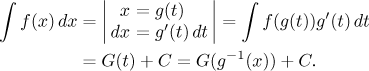
It looks as if we followed the above direct substitution in the opposite
direction and there is something to it. There we tried to simplify the
integral by replacing a (complicated) expression with a single letter, here
we make the integral more complicated, but the basic mechanism stays the
same: We choose a transformation and then use it to change the integral, we
also get an equality for changing the defferential int he same way, by
taking derivative of g and using it as a coefficient. However, deep
inside it is a different procedure, which can be seen for instance from the
fact that here requirements on g are more strict (in particular, it
must be invertible, unlike the situation in direct substitution).
There is also a difference in difficulty of various stages. The direct
substitution tight at the start, especially with replacing the dx
which often makes the chosen substitution impossible, but the back
substitution is clear. On the other hand, the indirect substitution has no
trouble with dx, from
x = g(t)
we immediately get
x = g′(t)dt,
but the back substitution can be quite an adventure, especially if we want
the answer in a nice form.
Now why would anyone want to make an integral more complicated then it
already is? Not surprisingly, the indirect substitution is used quite
rarely, but there are specific types of integrals where it does help and
experienced integrators know beforehand that certain indirect substitutions
will in the end magically simplify (see
integrals with roots
in Methods Survey - Integration).
We will show a very simple example of this kind.
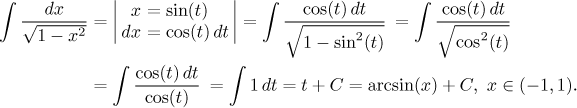
Actually, this is an elementary integral that one should remember.
Note that even this simple example is already good enough to
illustrate that the indirect substitution is not as simple as it looks. A
careful reader should get mightily suspicious at the first integral in the
second line: Shouldn't there be an absolute value in the denominator? That
is a very good question and the answer depends heavily on how we actually do
this indirect substitution. According to the theorem we are supposed to take
a function g = sin(t) that goes from
some interval J to our interval (−1,1). This interval
J must be chosen in such a way that g is 1-1 there and the
image of J under g must be the whole interval
(−1,1). The most natural choice is the interval
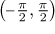 , so the
new integral, after the substitution, is considered on this interval. There
the cosine is always positive, so indeed, there is no need to
use an absolute value in the denominator when cancelling the square root and
the square power there. Note, however, that if we chose a different
interval for J, then we might be forced to use the absolute value.
As we see, this is another difference, in direct substitution we need not
worry about intervals used in the procedure.
, so the
new integral, after the substitution, is considered on this interval. There
the cosine is always positive, so indeed, there is no need to
use an absolute value in the denominator when cancelling the square root and
the square power there. Note, however, that if we chose a different
interval for J, then we might be forced to use the absolute value.
As we see, this is another difference, in direct substitution we need not
worry about intervals used in the procedure.
Mixed substitution
is a combination of direct and indirect substitution. We use it to shorten
calculations when we have to use several substitutions in a row. Experienced
integrators can save quite a lot of time this way. It starts with a
transformation
h(y) = g(x)
and the second important equality is dediced using the usual idea, we
differentiate on both sides and attach differentials:
h′(y)dy = g′(x)dx.
We present one example here that can be also solved by applying two
simpler substitutions one after another (try it, it is a good practice):
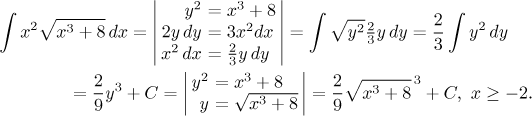
Also here one has to be careful on which interval the new variable lives, in
this particular example one has to decide between intervals
[0,∞)
and
(−∞,0],
since y2 is supposed to be 1-1 on the working
interval. It will not make any difference at the end, but it may strongly
influence calculations that get us there, we will see some of it below.
Substitution in a definite integral
This is basically the same as using substitution in an indefinite integral.
We state that the basic rule in substitution is to change everything from
the language of x to the language of y, and that include also
the limits. How do we transform them? As usual, using our basic
transformation
y = g(x). Example:
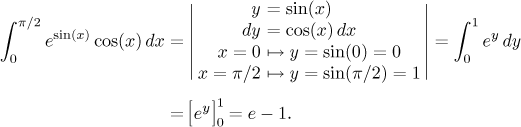
Similarly we change limits in the indirect and mixed substitution, but there
it is somewhat more difficult. For instance, we had a substitution
y2 = x3 + 8
above. If it were a definite integral and one of its limits was
x = 2, then we would substitute it into the
transformation equation and then look for corresponding y. In this
case there are two possibilities, plus and minus 4, the right one is
determined by the choice of the interval J in the substitution.
For practical hints and examples see
Substitution in Methods Survey -
Methods of integration.
Next section: integration by parts
Back to Theory - Integration
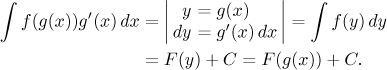
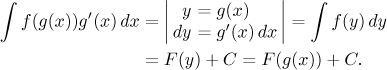
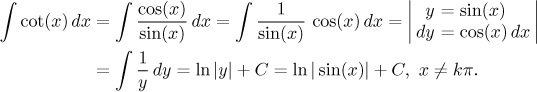
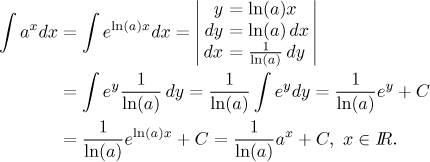
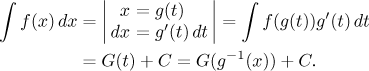
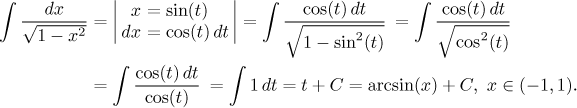
![]() , so the
new integral, after the substitution, is considered on this interval. There
the cosine is always positive, so indeed, there is no need to
use an absolute value in the denominator when cancelling the square root and
the square power there. Note, however, that if we chose a different
interval for J, then we might be forced to use the absolute value.
As we see, this is another difference, in direct substitution we need not
worry about intervals used in the procedure.
, so the
new integral, after the substitution, is considered on this interval. There
the cosine is always positive, so indeed, there is no need to
use an absolute value in the denominator when cancelling the square root and
the square power there. Note, however, that if we chose a different
interval for J, then we might be forced to use the absolute value.
As we see, this is another difference, in direct substitution we need not
worry about intervals used in the procedure.