Problem: Evaluate the integral
![]()
Solution: We started to solve this problem in this note as an example of substitution, we prepared it like this:
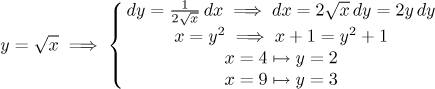
Why did we chose to do so? The root was clearly troublesome, so getting rid of it by substitution seemed like a good idea. Whether it will be possible or not depended on us being able to express dx solely in terms of y. We succeeded, thus we can pass to a new integral.
![]()
Were there any alternatives? When we go through "boxes" for various
types, we see that the given integral fits only the box "integrals with
roots". There the recommendation is to use the indirect substitution
The new integral clearly belongs to the box "rational function", so we use the appropriate procedure. Just to be sure that we do not work unnecessarily we check whether it is possible to cancel something in the fraction, but it does not look like it, so we start standard steps. Since the degree in the numerator is higher, we first apply the long division and then decompose the resulting remainder into partial fractions:
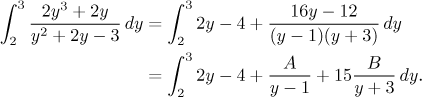
Since there are only linear factors, we easily obtain the unknown constants using the cover-up trick and the decomposition is done.

Since we know that a linear substitution always works, we see that
both fractions are essentially of the form
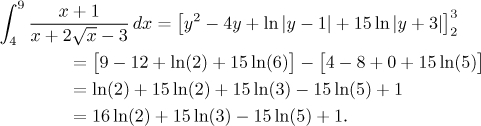
By the way, if the question asked for the indefinite integral (or if we decided to first find an antiderivative and then plug in the limits), we would get
![]()
We could put the logarithms together, but it would lead to a fifteenth power,
which would not look any better than what we already have, so we leave the
answer alone. The result is valid on all intervals of non-negative numbers not
including