Problem: Evaluate the integral

Solution: This integrals obviously belongs to the box "roots of quadratics", namely it is the type that we solve using the substitution A/cos(t). Because this often means a lot of work, we briefly consider alternatives. Other specialized boxes do not fit, the only remaining possibility is some substitution. There are two reasonable candidates, y = x² − 4 and y² = x² − 4. Both of them will only work if we can somehow work out a way to handle the expression x⋅dx. It is not present in the integral, so the only hope is in somehow algebraically express x using y. Experience suggests that this is not a good idea, and indeed the resulting expressions are so bad that the integral does not get simplified at all. Thus it is a blind alley, details can be found here.

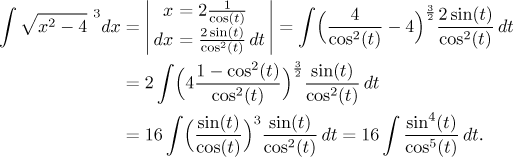
This integral obviously belongs to the box "trigonometric integrals". We have an extra cosine, which indicates that a sine substitution might be a good idea. We use the multiply-divide trick to move the extra cosine into the numerator, rewrite the rest into a formula involving only sines and then use the sine substitution:

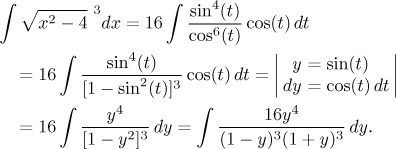
We obtained a rational function. We quickly check that it cannot be solved by substitution (the numerator is not close to the derivative of the denominator) and that we cannot cancel in the fraction. Then we start the partial fractions decomposition. By the way, we left the sixteen in the numerator to lower the chance that there will be fractions - calculations are then easier. We have two linear factors in higher power, therefore the general decomposition is

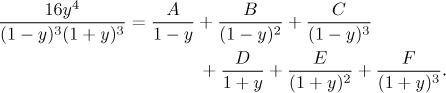
Two constants - C and E - can be obtained for free using the cover-up method, for the rest we need four equations. The multiplying method can do it, one can also simplify this work by some tricks. Since this part is routine, we leave the details as a note. We obtain the decomposition

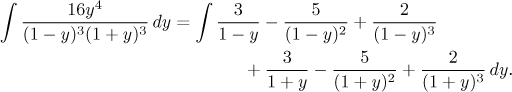
Now we integrate, experienced integrators do it right away (but be careful about the sign), those more careful will use substitutions s = 1 − y and t = 1 + y. You should get

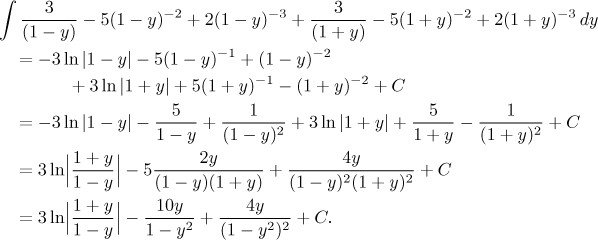
We did the last modifications because now we face the back substitution involving sine, so it is a good idea to make the process more friendly:

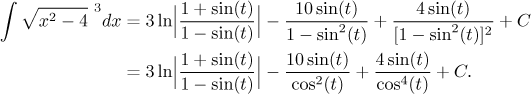
And now it is time for the second (and last) back substitution. First we calculate what to replace the sine with, it will involve a little cheating with absolute value that we discuseed in the section on appropriate box:

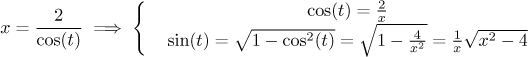
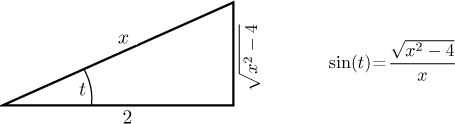
One can also get this formula using a suitable triangle, where we start from the formula for cosine above, fill in the third side and then easily deduce the sine.

Finally we get

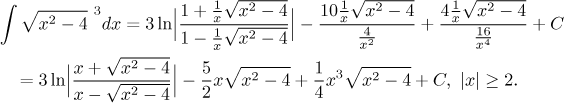
After such a long calculation (and a bit of cheating) we really have to check that the answer is correct, especially that there is no problem when x is negative. Differentiation shows that it is fine.

In the box "roots of quadratics" we also mentioned an alternative procedure, namely Euler substitutions. Here we can use the first one and obtain:

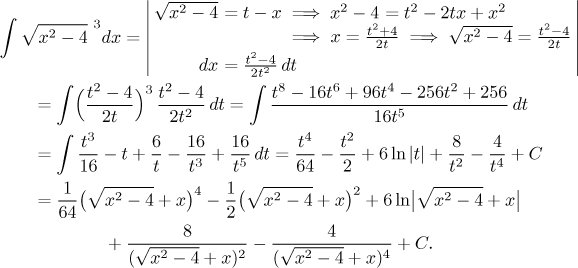
The calculations vere surprisingly simpler, but the result looks quite intimidating. Is it the same as the first result? Actually, it is, but showing so is not quite simple, see this note.

Since the quadratic expression under the root can be factored, we can also use both versions of the 3. Euler substitution:

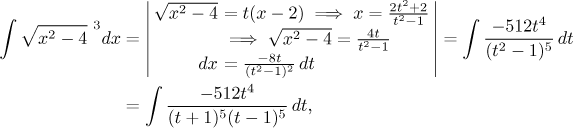
or also

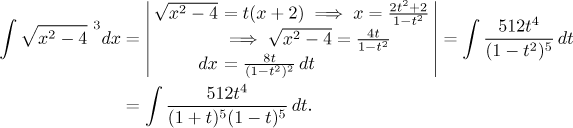
This approach ended up with integrals similar to our first approach, but the powers in the denominators are higher by two, so the partial fractions decomposition would require eight equations, not something we would like to do. This is not a good idea.

Another alternative solution we mentioned is the hyperbolic substitution:

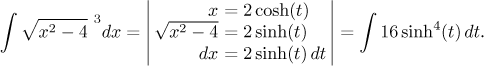
Integration of hyperbolic functions was briefly covered in the box "trigonometric integrals" and we recommended to treat them similarly to trig integrals. In this particular case we could use reduction formulas, which can be deduced or found in some thick math book. Since we do not have any list of integrals handy, we try a different approach: reduction of powers using hyperbolic identities, which may be slightly different but definitely very similar to corresponding trig identities. Multiples of argument are then handled using linear substitutions:

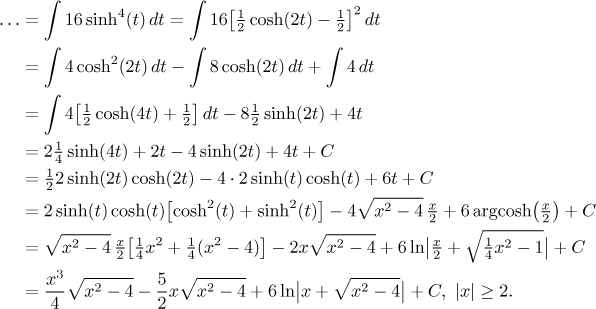
This answer can be relatively easily rearranged to fit our first result, it is enough to fix the logarithmic term and we already did it in this note.

Next problem
Back to Solved Problems - Integrals