Problem: Evaluate the integral
![]()
Solution: There are four approaches to this problem! It exactly fits the box "rational function", so we start with the appropriate algorithm. First we have do the long division and then decompose the remainder into partial fractions. It turns out that this is not necessary as the remainder itself is a partial fraction already, so we can integrate right away.
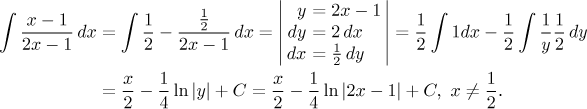
Note that theoretically we defined partial fractions to feature expressions
of the form
![]()
But it is not necessary, it can be shown that a constant next to the variable does not spoil anything, one just has to be careful when integrating.
Now we explore alternatives. First, there is a simple way to avoid long division of polynomials for those who do not quite like it. The trick is simple, use algebra to create the expression from the denominator also in the numerator (see the add-subtract and multiply-divide tricks here). The calculations go
![]()
In the integral it looks like this.
![]()
Of course it yields the same result as above, but some people may find it easier.
Another interesting alternative is to simplify the denominator so that we can divide by it easily. One could also call it moving the subtraction into the numerator, it is done by a simple substitution.
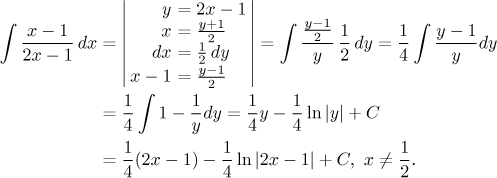
It is easy to change the answer to the form we had above.
This problem also fits in the box "ratio of linear functions". We apply the recommented substitution.
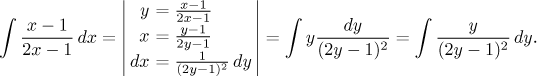
We are now integrating a rational function which has just one linear factor in the denominator, but in a higher power. One constant in the decomposition can be obtained using the cover-up trick, then one need one equation, which can be easily obtained using the limit trick. We multiply the general decomposition by y and then send y to infinity. If you want, you can use the multiplication method, we will show it as an altermative.
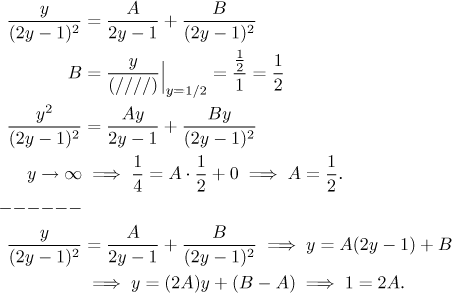
Now we finish the calculation using an obvious substitution, an experienced integrator would write the integrals right away, but it may be a good idea to do these substitutions properly in order not to forget some constant.
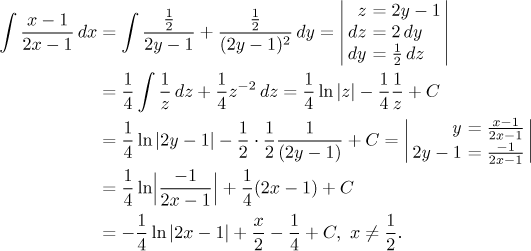
We got the same result as before.