Problem: Evaluate the integral

Solution: When we look at an integral we usually first think of substitution. Here an idea occurs to simplify the composed function by substitution, usually we take for y the inner function x². To succeed we would have to find x⋅dx in our integral, which is easy to arrange by borrowing one x from the power.

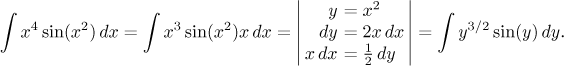
This would look like the perfect integral for integration by parts, namely the type "removing powers", but for a small detail: The power at y is not an integer. Therefore we cannot make it go away using differentiation and integration by parts fails. No other reasonable solution presents itself, so this substitution worked, but it lead to an integral that we cannot solve with our tools.

We have to look for some alternative. His integral does not fit into any box related to special types, and concerning basic methods we already ruled out substitution and partial fractions are obviously no good here. What remains is integration by parts.

This actually seems like the natural choice. The integrated function is already written as a product, one part of which is a power of x that can be removed by repetaed differentiation. However, we run into trouble with the second requirement that the other part should be easily integrable. Let's see: We choose the natural choice.

Now we easily find f ′(x) = 4x³, but then we run into trouble, because we need to find

and this integral cannot be evaluated by any of the methods we cover here. Why is it so? The only reasonable substitution would be y = x², but to make it work there is x⋅dx missing in the integral. If we try to create it with algebra, it ends up with another unsolvable integral, try it as an exercise, see here. Methods from other boxes do not fit.

Now we try to switch the functions:

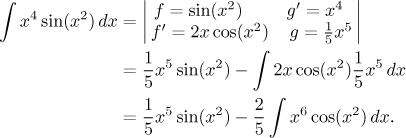
Here we managed to calculate the necessary expressions and use integration by parts; however, the new integral we obtained is even worse than the one we started with.

What is the right way then? The key to success is our very first attempt. When we tried the natural setting for integration by parts, we had troubles getting g. However, we saw that integration works if we have an extra x.

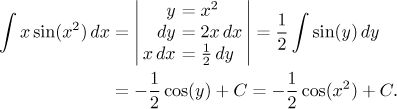
That extra x is easy to arrange, we move one x from f to g′. Finally we are getting somewhere.

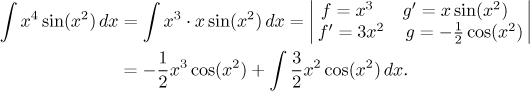
Yes, that's how it is supposed to work, the integral stayed basically the same but the power at x decreased. So it's one more time.

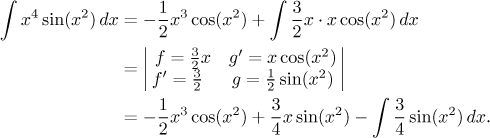
We ended up with an integral that we gave up on earlier. Given that this was our last chance, it is time to ask whether we are sure that none of our tricks would work on this one. Unfortunately, the answer is in the positive. Not just our methods, it is known that the integral of sin(x²) is one of those that surely exist, but it cannot be written using elementary functions and operations. Plainly told, this integral is not solvable using classial methods. Our calculations show that this unsolvable integral is equivalent to the one we were given, so also our problem is not solvable using classical methods.

Since every integration by parts decreases power by two, we see that when we integrate x^ksin(x²) and k is an even natural number, then the problem cannot be solved. On the other hand, if k is odd, then integration by parts (eventually) decreases the power to 1 and such integrals can be handled easily, see above.

So much for classical methods. How about some non-classical methods? There is a way using power series. We expland the sine and the rest is easy (if you know how to handle infinite series).

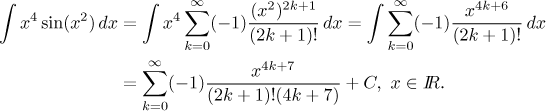
This answer is not exactly what we usually accept, but there are applicacions where this is preferable to no answer.

Next problem
Back to Solved Problems - Integrals