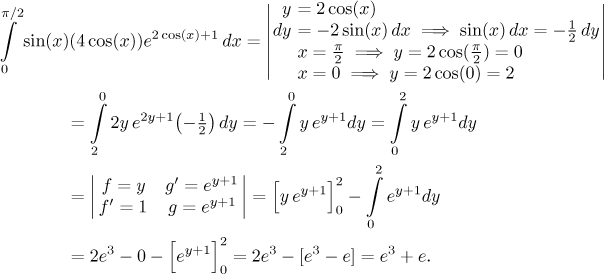Problem: Evaluate the integral
![]()
Solution: This integral does not fit into any specialized box (rational functions, roots, trig functions etc.), so it should be approached using basic principles, preferably substitution. Is there any candidate? In fact there are several good candidates, prime suspect being the inner function in the compose exponential. In a typical case we would denote the exponent as y and then ask whether we find its derivative next to dx. The derivative is (up to a constant) equal to sine and we do have a sine in our integral that can be moved to the right, so it seems that there will be no problem.
Since substitution and a definite integral work well together, we will keep the limits, but we do have to change them into the new variable.
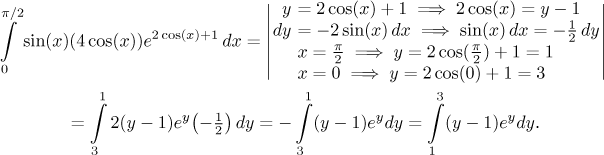
Now this is a clear cut case for integration by parts, a perfect specimen of the type "removing powers". We therefore proceed accordingly, we will denote the polynomial as f and get rid of it by differentiation.
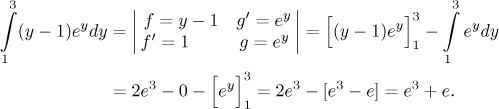
That was simple. Just out of curiosity, if the integral was given as indefinite, then we would get
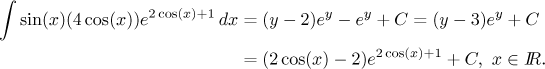
We talked of more substitutions, which are these? Usually it pays to be modest and focus on the heart of a problem, in this case on the cosine in the exponential. Substitution is then easier, but integration by parts is a bit more complicated.
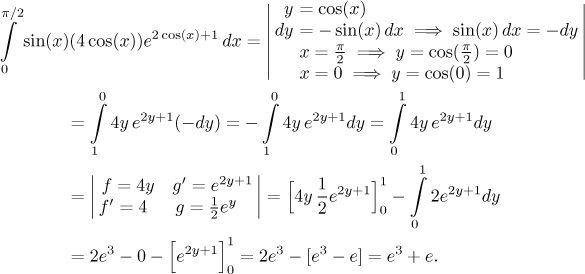
The key problem here is integration when determining g. An experienced integrator knows it right away, so it does not delay him and this way of solving this problem seems optimal, because there is no messing around with constants while doing the first substitution.
One can also go for a compromise.