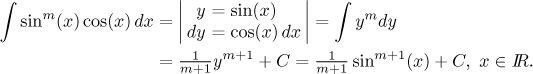
We will start with the sine formula. First we evaluate an auxiliary integral that will be used later:
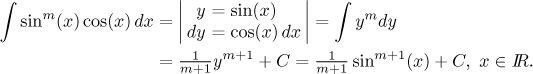
A power of sine is integrated by first using a trig identity and then applying integration by parts:
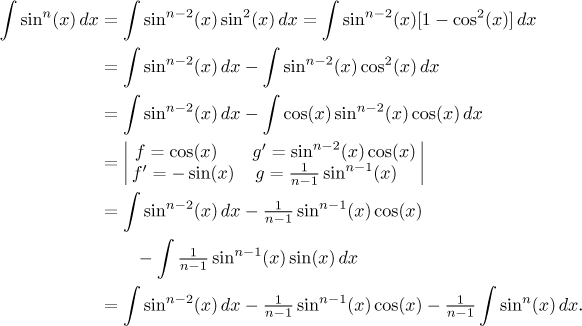
We get an equation. To solve it, we move the integral from the n-th power from the right hand-side to the left:
![]()
By moving the fraction from the left hand-side to the right we obtain the desired reduction formula. The reduction formula for the n-th power of cosine is deduced similarly.
Now we pass to a power of tangent. This can be integrated directly by a substitution, after first using an algebraic trick:
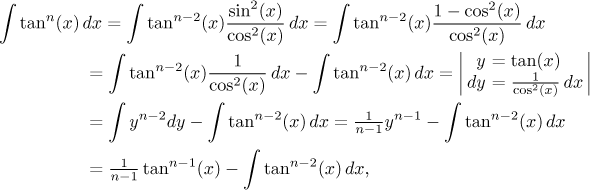
exactly as we stated. The cotangent formula is obtained in a similar way.
It remains to evaluate the integral of a power of secant (cosecant is handled similarly). This requires an algebraic trick and integration by parts, but we will not have to solve equations. First we need one auxiliary integral:
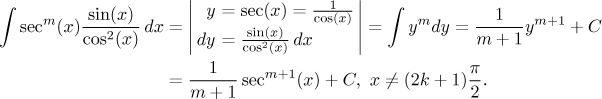
And now we can do the calculation itself:
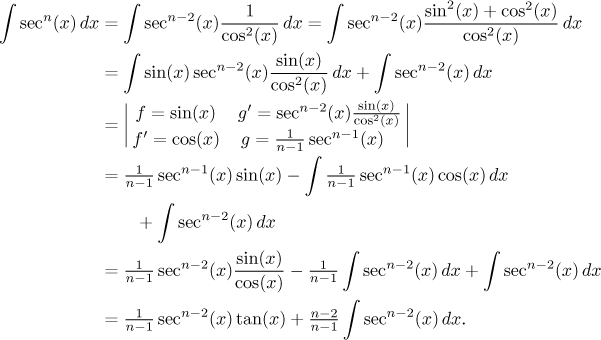
Try to deduce reduction formulas for cosine, cotangent and cosecant; it is a good exercise.