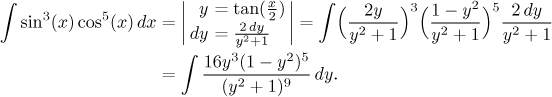Example:
![]()
We will try to solve it purely by the recommended approach using identities where we reduce powers by trading them for multiples of variable.
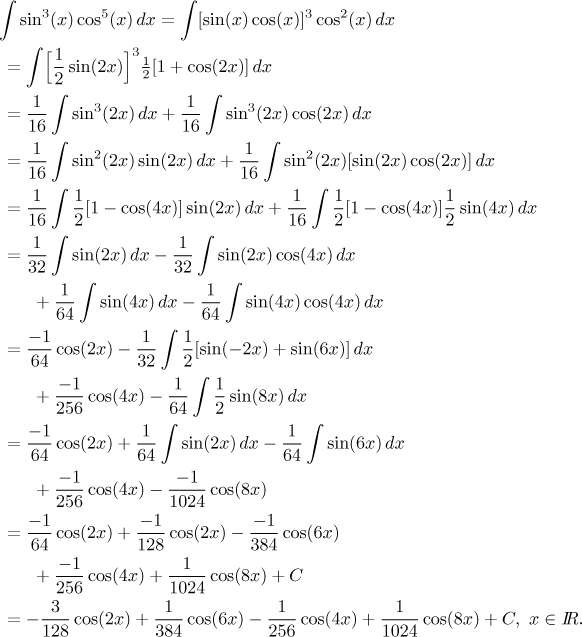
It was very long, but as we promised the calculations indeed ended up with integrals that could be solved using linear substitutions. Are there any alternatives?
An experienced integrator would take a different route on the third line. There is an "extra cosine" in the integral on the right, clearly pointing to sine substitution. The left integral is just a power of sine, so one can approach it using the appropriate reduction formula, but few people remember it, a more usual approach would be to take one sine away as "extra sine" and change the rest into cosines, thus getting ready for cosine substitution.
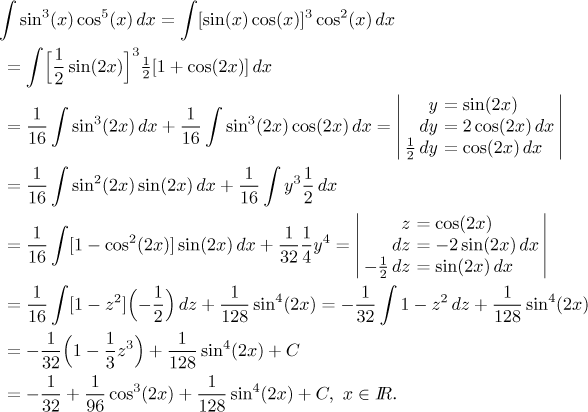
As expected, it was shorter, even though we wrote all the details; an experienced integrator would do much of it in his head.
Is there any other alternative? How about right at the beginning? Actually, not really. In the given integral, both trig functions have odd power, which is the worst situation possible. Of course, one can always use the universal substitution, but as usual it leads to an integral that we prefer not to see ever again.