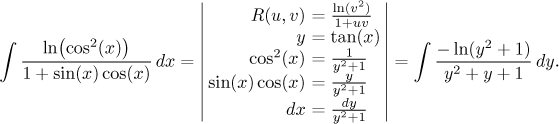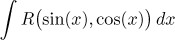 ,
where
,
where
Consider an integral of the type
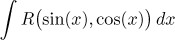 ,
where
,
where
1. If for all u, v on the unit circle we have
This in fact means that we consider integrals of the type
![]()
where the function G itself does not feature trigonometric functions.
Example:
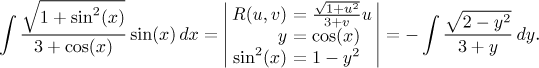
2. If for all u, v on the unit circle we have
This in fact means that we consider integrals of the type
![]()
where the function G itself does not feature trigonometric functions.
Example:
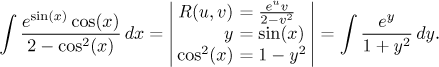
3. If for all u, v on the unit circle we have
This in fact means that we consider integrals of the type
![]()
where the function G itself does not feature trigonometric functions.
Example: