Example: Decide whether the following integral converges:
![]()
Solution: We check that there is just one problem, the infinite upper limit. Therefore we have an improper integral of the basic type and we can apply convergence tests. First we decide on a test function. This should be easy, in the numerator and denominator we have polynomials and we know that when x grows to infinity, only the highest powers prevail.
First we try to see whether there is an inequality possible:
![]()
There is an inequality, so we can try to apply the Comparison test. We check
on the test integral, which is easy: We remember the scale of powers and
therefore we know that
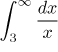 diverges. Unfortunately, this is exactly the situation when the Comparison
Test does not yield a conclusion. Intuitively, the inequality between
functions translates to
diverges. Unfortunately, this is exactly the situation when the Comparison
Test does not yield a conclusion. Intuitively, the inequality between
functions translates to
![]()
This inequality would be satisfied if the given integral was equal to a number but also to infinity, so we do not know. The Comparison test failed.
Now we try the Limit Comparison test. We feel that for really large values of x,
![]()
This guess has to be justified:
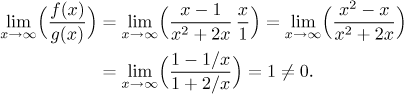
So the functions are indeed about the same near the problem point. Since the
test integral
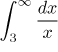 diverges, by the Limit Comparison test, also the given integral diverges.
diverges, by the Limit Comparison test, also the given integral diverges.