Problem: Find the area of the region
![]()
Solution:
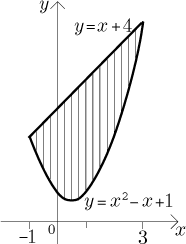
First we need to identify the region. We have to find for which x the
inequality makes sense, that is, for which x the function
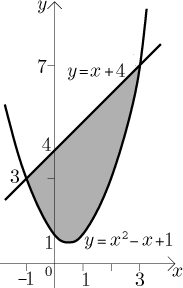
This region has the right shape, therefore we can directly integrate, we have to remember to put correctly the larger function minus the smaller one:
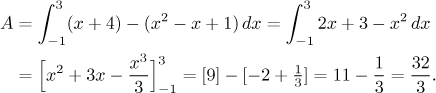
Now we will try it another way, we switch the axes. First we need to find
inverse functions. Note that it is not possible to find an inverse function
to the quadratic function, as it is not one-to-one on
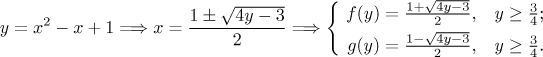
Thus we have:
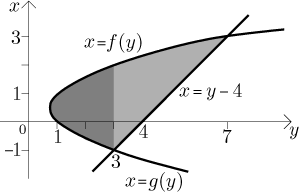
Now we see that the region is not of the basic type, because its lower side is defined not by one, but by two functions. To find the area, we have to split the region into two parts, as suggested in the picture. Thus we get
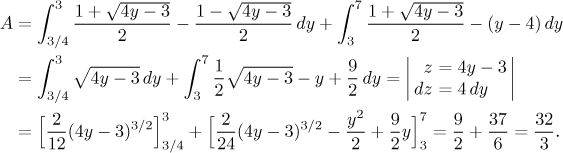
Remark:
Here we will try to explain how one can set up integrals easily without
relying on memorized formulas. First we will try vertical slices.
We get the total area by adding the areas of the strips, that is, by adding their lengths multiplied by the width dx. Since each strip is determined by a chosen value of x, we add them up by changing x, that is, by integration with respect to dx. The length of a strip is equal to the y-coordinate of the top minus the y-coordinate of the bottom, but since we integrate with dx, this information must be supplied in terms of x. Fortunately for us, that is exactly what we have in the picture. We thus get
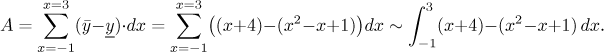
Now we will try horizontal slices.
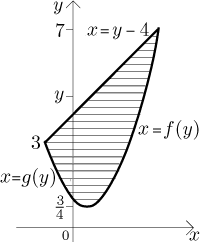
Again, we get the total area by adding the areas of strips. Now their thickness is dy, also the position of one particular strip is determined by fixing the variable y, which suggests that we should add all strips by changing the variable y; from the picture it seems that we should go from 3/4 to 7. Adding means integrating, so we will integrate with respect to y. This seems clear, we are changing y to go through strips, also the differential dy appears in our considerations.
For a given strip (corresponding to a fixed value of y), its length is equal to the x-coordinate of the upper (right) end minus the x-coordinate of the lower (left) end, and since we integrate with dy, this information must be supplied in terms of y. The ends of strips lie on the given curves and we need to put this information in the form x is equal to some formula with y. This means that we have to pass to inverse functions to the given ones. But since the left ends of strips are not all on the same curve, we have to consider two different kinds, leading to two integrals. Thus we get
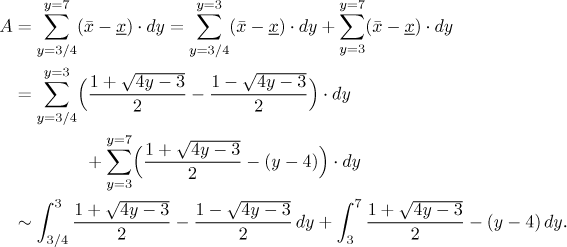
We used this example to show how to decide whether to use vertical slicing (integration with dx) or horizontal slicing (switching the axes, integrating with dy). We always try to use the alternative that has nicer functions to integrate, and if possible, we pick the alternative where the strips are of fewer kinds. The best possible case is when there are strips of just one kind, which means that the whole region can be handled using just one integral.