Problem: Consider the finite three-sided region R bounded by the graphs of
![]()
Find the volume of the solid obtained by revolving this region about the
axis given by
Solution: First we draw a picture:
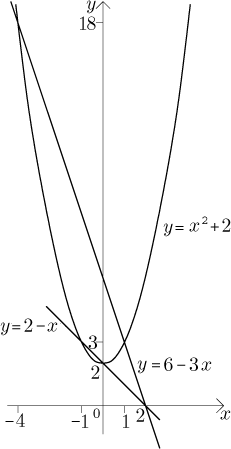
There are many regions bounded by the three curves, but only two of them are finite and just one of them has three sides. We will try to slice it vertically.
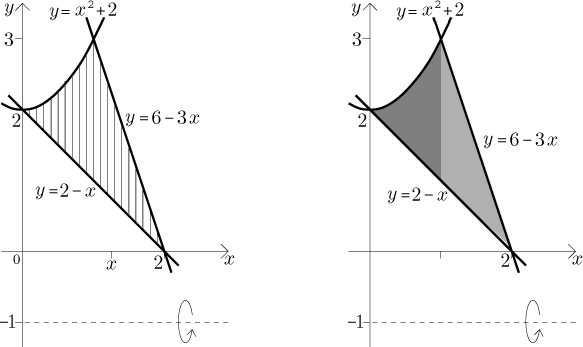
By rotating the strips we get discs (with holes), meaning that we can find the volume using the disc method and integrating with dx (or we just remember that horizontal axis of rotation means the disc method). However, we see that the strips have upper ends of two different kinds (that is, the upper side of the region is defined by two different functions), which means that we have to split the region into two regions of the basic type. We get
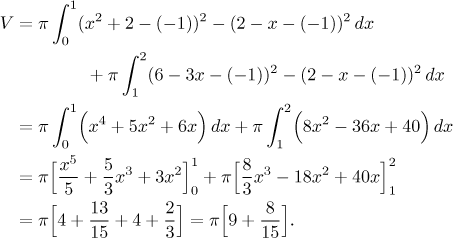
The region has a shape that is not of the basic type even if we switch the axes:
Now we have a vertical axis of rotation, so we should use the shell method, and again, we have to split the region in two and use two integrals:
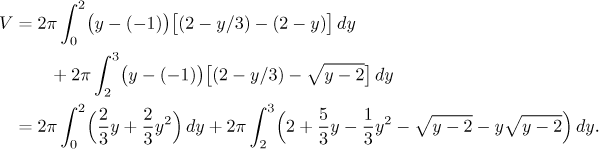
This integral seems somewhat more difficult than the one from the disc
method, but it is not too bad, the square roots are easy to integrate using
the substitution
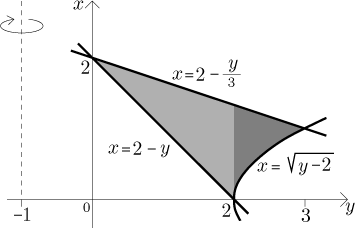
In fact, one does not have to switch the axes to set up the integrals with dy. Consider the original picture, but with horizontal slicing:
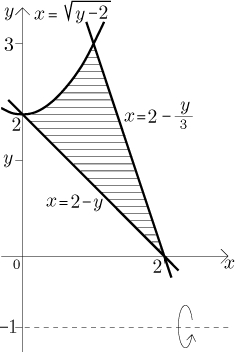
Strips have thickness dy, which shows that we will have to integrate with dy. A certain strip is fixed when we fix some value of y. The length of such a strip is equal to its upper (right) x-coordinate minus its lower (left) x-coordinate, these have to be expressed in terms of y. This naturally leads to the inverse functions for the curves, and since there are two different kinds of left endpoints, we need two integrals, first y goes from 0 to 2, then from 2 to 3 - in this way we cover all strips.
What happens when we spin one such strip about the line