Root and Ratio test

There is one type of a series that we know quite well - the geometric series. Thus it can be very helpful if we learn that a given series is similar to a geometric series. The Root test and the Ratio test are at their hearts two ways to recognize such similarity. We first show the most popular type of these two - the limit version.

Theorem (Root test - limit version).
Consider a series  ∑ a_k  such that a_k ≥ 0 for all k. Assume that the limit

converges.
• If ϱ < 1 then the series converges.
• If ϱ > 1 then the series diverges.

It is also called D'Alambert's test. Why does it work in this way? The limit result says that for really large k we essentially have

So a series that satisfies the assumption of this test really looks like a geometric series (for large k, that is, at its end, but we know that convergence is decided at the end of a series). Now the conclusion should be obvious (or at least believable). What about the case ϱ = 1? The Root test gives no conclusion. In that case the terms of this series are more or less like 1^k. The corresponding geometric series is divergent, but it is the borderline case between convergence and divergence. Since the terms of the given series are not exactly equal to 1^k but might be a bit larger or a bit smaller, it follows that convergence depends on how exactly do the terms of this series move about the number 1, therefore it is highly individual and one cannot expect a general rule for this case.

Theorem (Ratio test - limit version).
Consider a series  ∑ a_k  such that a_k > 0 for all k. Assume that the limit

converges.
• If λ < 1 then the series converges.
• If λ > 1 then the series diverges.

It is also called Cauchy's test. Why does it work in this way? The limit result says that for really large k we have

Here it is not as obvious as in the case of the Root test. For simplicity assume that the approximation in the limit works for all k, not just for the large ones, then we can go like this:

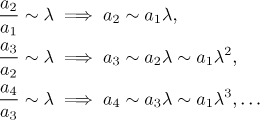
Again, notice that the case when lambda is 1 remains unsolved. However, here one can get some help from a more sophisticated test, see the Raabe test in the section Theory - Testing convergence - More tests.

Example: Investigate the convergence of  .

We apply the Root test.

(For the limit of k^1/k see the Fact below.) Since ϱ < 1, the given series converges.

We will try to independently confirm this conclusion by applying the Ratio test.

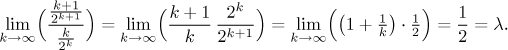
Since λ < 1, the given series indeed converges. Note that when evaluating the limit, we grouped together in separate fractions terms with the same "origin"; this is typical and usually very helpful.

Note also that the two constants in the Root test and in the Ratio test came up equal. This is always true (that is, when both tests can be used) and it is not really surprising. Each tests essentially answers the question "to which geometric series is this one similar", and the same series cannot be similar to two different geometric series. Theoretically, the Root test is "stronger" in the following sense: If the limit for λ converges, then also necessarily the limit for ϱ converges (and to the same number). Thus, theoretically, if the Ratio test works, we can always do the Root test instead. On the other hand, there are series for which the limit for ϱ converges but the limit for λ doesn't and the Ratio test cannot be used. However, this only talks about theoretical convergence, finding limits in practice may be another story. There are cases where applying the Ratio test is simple but the limit for the Root test is a real killer.

When using the Root test one often uses the fact that the k-th root of k goes to 1. It can be generalized as follows.

Fact.
Consider a non-zero polynomial p(x). Then

From practical point of view this means that when a series is based on polynomials, then usually the Root test and the Ratio test do not give us anything about its convergence. What really works well with these two tests are series that feature expressions of the form 2^k, as we saw above. For hints on choosing the best test see Methods Survey - Testing convergence.

The limit versions of the two tests that we saw above are simple to use, but they are not the strongest available. There are cases when they fail not because they yield 1, but even before we get there. We know that not every sequence has a limit, so it may happen that we do not even get any rho or lambda. We will show two ways to fix it.

There is a notion of a limit that is more general, so-called "limes superior". It is known that every sequence {c_k} has "limsup", so this notion is more reliable; also, if a sequence converges, then its normal limit is also limsup. Can we use it in the above tests? It turns out that in the Root test we can simply replace "lim" with "limsup" and everything works as before. This is surely useful and in some books you will find this test stated in this form.

On the other hand, only the first statement - about convergence - can be done using limsup in the Ratio test. So this is still useful, but not as elegant. For precise statements see this note.

Probably the most elegant and at the same time the most general versions of these test prefer to look at terms as individuals, not through some limit notion.

Theorem (Root test).
Consider a series  ∑ a_k  such that a_k ≥ 0 for all k.
• If there is ϱ < 1 and an integer N such that    for all k > N, then the series converges.
• If    for infinitely many k, then the series diverges.

What case remains indeterminate? If the terms a_k^1/k are strictly less than 1, but they approach 1 arbitrarily close.

Theorem (Ratio test).
Consider a series  ∑ a_k  such that a_k > 0 for all k.
• If there is λ < 1 and an integer N such that    for all k > N, then the series converges.
• If there is an integer N such that    for all k > N, then the series diverges.

If you are curious about relationship between this "inequality" approach and "limsup" approach, check out this note.

For more information see Root test and Ratio test in Methods Survey - Testing convergence and also Solved Problems - Testing convergence. Namely, typical situations of using the Root test can be found in this problem, this problem, this problem, and this problem, check out also this problem. For the Ratio test check out this problem, this problem, this problem, this problem, and this problem, try also this problem.

Note about general series: If a given series ∑ a_k does not have terms with equal signs (they are not either all positive or all negative), then the Root test and the Ratio test can be only applied to the absolute value version  ∑ |a_k|. If ϱ < 1 (or λ < 1), then the series  ∑ |a_k|  converges and therefore automatically the series  ∑ a_k  converges (see Absolute convergence in Theory - Introduction).

If ϱ > 1 (or λ > 1), then the series  ∑ |a_k|  diverges. In general this does not tell us anything about the original series  ∑ a_k, but in this special case we can actually pass divergence to it by the following argument.
It is easy to show that if ϱ > 1 (or λ > 1), then |a_k| goes to infinity, which in particular means that a_k does not go to zero and therefore, by the necessary condition, the series  ∑ a_k  diverges. In this way we actually obtain general version of these two tests, but that belongs to the section Convergence of general series.

Comparison tests
Back to Theory - Testing convergence