Comparison tests: Methods survey

We use comparison tests for series whose terms have parts that we want to ignore in our considerations. The basic idea is that when given a series that we do not quite like, we pass to a series (test series) whose convergence/divergence is already known or at least is easy to determine. This information about the test series is then passed on to the given series, which is however not always possible.

Note that "series whose convergence is known" most often means the p-series, that is, series with terms 1/k^p. The p-test says that such a series converges exactly if p > 1. Thus we usually try to compare the given series to such a suitable p-series, but sometimes we may also choose a different test series.

Precise statements concerning comparison tests can be found in the section Comparison tests in Theory - Testing convergence, here we focus on practical approach.

There are essentially two basic situations.

1. Plain comparison: Sometimes we have a series that features parts that are bounded, then one can replace them by something nicer. Typical examples would be series whose terms include sin(k) or cos(k). Then the plain Comparison test is exactly the right thing.
Some other time we may want to simplify a complicated expression by simply ignoring some of its parts. If this leads to a general increase in terms (or decrease), again this is something that Comparison test can handle.

The basic idea of Comparison test is that an inequality can pass from individual terms to series:

then one can use common sense to get some conclusions: If there is a finite number on the right, then it must also be on the left; if there is infinity on the left, then it must be also on the right. By the way, we use capital letters for a very good reason: Here we traditionally denote the series we investigate using a_k, but in the above inequality it may appear as either one, the larger or the smaller one. Thus it would be confusing if we also used a's in the above inequality.

The main problem with Comparison test is the fact that it only works "one way". Thus not every comparison between series that we obtain can be useful. Sometimes we do not have much choice, the comparison is somehow forced on us by the situation, then we can only hope that it proves itself useful. An example of this can be found in this problem in Solved problems - Testing convergence.

However, sometimes we have more options and in that case it is very helpful if we can guess the answer, because it helps to guide our reasoning. The procedure then goes as follows.

Algorithm:
You are given a series  ∑ a_k  with non-negative terms. You prefer to pass to another series  ∑ b_k  with non-negative terms.
• If you suspect that the given series converges, then look for an upper estimate to force it down, that is, look for b_k such that a_k ≤ b_k and  ∑ b_k  converges.
• If you suspect that the given series diverges, then look for a lower estimate to force it up to infinity, that is, look for non-negative b_k such that a_k ≥ b_k and  ∑ b_k  diverges.

The main advantage of Comparison test is that the terms b_k need not be very similar to a_k (unlike the limit comparison), which offers more flexibility.

The core of this test is the guessing part. There we use our experience with intuitive reasoning, we replace the given expression with its dominant term(s). However, to be reliable, such guessing has to be confirmed, and to confirm that two quantities are the same for k near infinity we use the natural idea: We divide the two quantities and send k to infinity. If the two quantities are the same, we expect to get 1, but in fact any positive number would do.

Algorithm:
You are given a series  ∑ a_k  with non-negative terms that can be simplified for k large.
Step 1. Take a guess to find a candidate for a test series; that is, guess that when k approaches infinity, then a_k are pretty much the same as the positive numbers b_k.
Step 2. Confirm your guess by calculating

the limit must yield a positive real number (typically 1, but not necessarily).
Step 3. Investigate convergence of the test series  ∑ b_k. The conclusion (whether it is convergent or divergent) is also true for the given series  ∑ a_k.

The main advantage of the Limit comparison test is that its formal statement is an equivalence, that is, information is always passed from the test series to the given series. This makes this test very robust. There are two disadvantages. One is minor, compared to the Comparison test we usually have to do more work here (evaluating the limit). The other disadvantage lies in the necessary closeness of a_k and b_k which may prevent one from more creative comparisons.

Example: Determine convergence of the series

There is a natural comparison, namely

Unfortunately, the test series on the right is a harmonic series which is known to diverge (p-test), which is exactly the situation when comparison fails. Indeed, the above inequality then reads that the sum of the given series is less than or equal to infinity, which is true both when the given series converges and when it is infinite.

Intuitive reasoning suggests that the above comparison is very faithful, that for large k the two expressions come up basically the same, so one would guess that the given series diverges. If we wanted to prove this by plain comparison, we would have to find a lower estimate for it to push it up, but such an estimate is less obvious here since we go against the "natural" direction that we have shown above. We could actually try this:

The comparison between terms is not too hard to prove, it is based on the fact that for natural numbers, the square root is always dominated by the number itself. Now the series on the right is both smaller than the given one and gives infinity, which proves that the given series is divergent.

The above reasoning also looks like an invitation to Limit comparison. We claim that for large values of k we have

This needs to be confirmed:

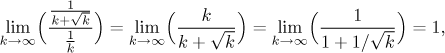
which justifies our claim. Thus the given series and the harmonic series behave the same, and since the latter is divergent, then so must be the given one.

For other examples see this problem, this problem, this problem, this problem, this problem, and this problem in Solved Problems - Testing convergence.

Root test
Back to Methods Survey - Testing convergence