Problem: Determine whether the following series converges.
![]()
Solution: The terms of this series are positive, so we can use all the wonderful tests. Since we definitely would not want to integrate the expression in the series, the Integral test is out. What about the other tests? Since exponentials beat powers, the terms of this series go to zero, so the series might converge but also not - the necessary condition does not help here.
The terms of this series consist of powers and exponentials, which is usually a good indication that either the Ratio or the Root test may help. Since taking the k-th root of the given expression does not look too inviting, we will try the Ratio test. When evaluating the ratio in the test we will use the popular trick of playing similar expressions against each other.
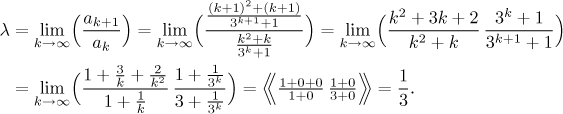
To find the limit we factored out dominant terms, which is the standard treatment for limits of ratios with powers and similar terms, see the corresponding box in Sequences - Methods Survey - Limit.
Since
Alternative:
What happens if we try the
Root test? We know that the
k-th root of a polynomial goes to 1, so that takes care of the
numerator. In the denominator it is a bit worse, since
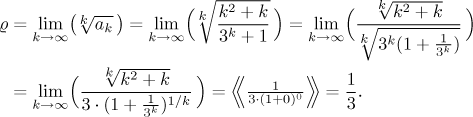
Since
Alternative: If it wasn't for the "+ k" and "+ 1" parts, the Root test would be very simple. Intuitive evaluation tells us that these two parts do not make any difference for large k anyway, which brings us right to the Limit comparison test. First we have to prove that these two parts can be indeed ignored by evaluating the appropriate limit.
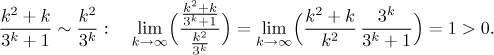
We obtained a positive number, so the terms are really comparable (we actually got 1, which shows that for large k the two terms are pretty much the same). Therefore also
![]()
Since the series on the right converges (apply the Root test), also the series on the left converges.
Could one use the plain Comparison test? In order to prove convergence we need an upper estimate. The denominator is helpful, since by ignoring the "+1" part there we make it smaller and thus obtain a simpler upper estimate for the whole term. However, simplifying the numerator is less obvious. If we remove the "+ k" part there, the resulting expression is smaller, which is exactly the opposite of what we need. Fortunately we can use a little trick, since natural numbers k can be majorized by k2.
![]()
And since the larger series on the right converges, so does the smaller given series.