Problem: Determine whether the following series converges.

Solution: This is obviously an alternating series, so we try the Alternating series test. We have

which is a sequence of positive numbers. Is it decreasing? The easiest way to check is to look at the derivative of the corresponding function.

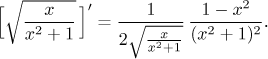
This derivative is negative for x > 1 and therefore the function (hence also the sequence {b_k}) is decreasing, see for instance Monotonicity in Derivative - Methods Survey - Graphing functions. This series therefore satisfies the technical assumptions of AST and it remains to check on the last one, that {b_k} tends to 0. But that is quite clear, the leading power in the denominator is higher than the power in the numerator, proper calculations can be done for instance by cancelling k, see the box on powers at infinity in Sequences - Methods Survey - Limit.

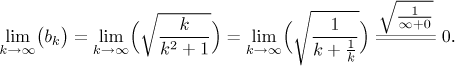
This proves that by the Alternating series test the given series converges.

Remark: The above solution is short and perfectly satisfactory, yet out of curiosity, is there an alternative? Another option is to try the absolute convergence angle. What can we say about the following series?

Since the terms of this series consist of polynomials, we know that both the Root test and the Ratio test come up indecisive. Indeed,

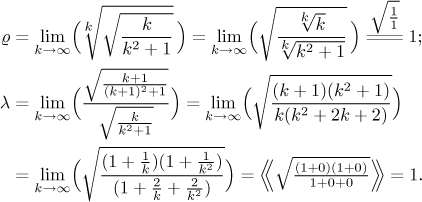
Since we do not like the idea of integrating the square root, the Integral test is also out. What is left? Actually, for series with polynomials the standard approach is via comparison tests.

How does the series behave? When k is large, then the terms look like

Note that the test series on the right is a p-series that diverges by the p-test. This means that there is in fact no need to work the comparison tests further. A divergent test series means divergent series on the left. This would mean that the absolute convergence testing we were just working on ends up negative; the given series does not converge absolutely. However, that is exactly the situation that does not allow us to say anything about the given series (we have the opposite implication: If a series converges absolutely, then it also converges). Therefore the whole approach to the given series via absolute convergence is a blind alley and there is no need to go on.

For completeness we work out comparison tests. First we do the Limit comparison test, we have to start by confirming that our guess above about behavior of a_k for large k was correct.

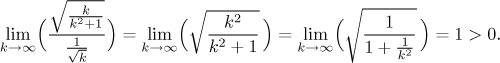
The comparison is confirmed and now we can make our conclusion:

If we tried the plain Comparison test, we would need to establish some inequality between the given terms and the test terms (or similar ones). One suggests itself.

However, this comparison is useless, since the larger series being infinite implies nothing about the smaller series on the left. In order to prove that series diverges one needs a lower estimate. There is one possible, but it is not an obvious one any more.

So the Comparison test also confirmed divergence (and thus no absolute convergence) and we are done with the failed alternative.

Next problem
Back to Solved Problems - Testing convergence