Problem: Determine whether the following series converges.
![]()
Solution: For positive integers k, the ratio
There is no obvious angle to this series. Integrating does not seem easy, taking the k-th root of sine does not look good, working out ratio of complicated sines either, and there seem to be no parts to ignore for comparison. So where do we start? We usually have good results with the Root test. As expected, the sine part leads to trouble, namely to an indeterminate power. We can work it out for instance like this:
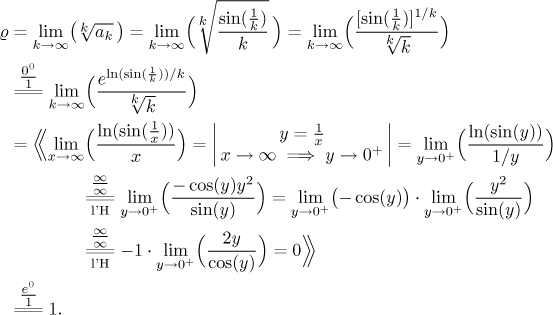
So after all that hard work we got the indecisive case
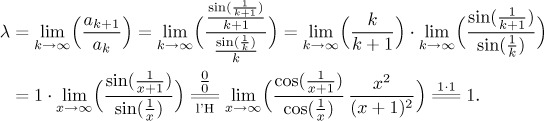
This actually seemed a bit easier. Given that these two tests did not help,
what else can we try? The idea of integrating the given expression is not
too appealing, but we are slowly getting desperate and after all, sine and
powers are not all that bad. Can we use the
Integral test? Yes, since the
function
What is left is
comparison tests. No part of the
given expression can be ignored for large k, but perhaps we can do
with an estimate, the sine suggests a natural upper bound. For k a
natural number we have that
![]()
We have a divergent series on the right (it is the famous harmonic series or use the p-test) and the given series is smaller, which is exactly the situation when comparison does not help.
Is there something else we can do? There is one test we did not try, the limit
comparison. It does not seem very suitable, but we are getting desperate. What
do we know about the terms ak when k gets really
large? Then
![]()
Of course, the Limit comparison test requires that we justify our guess, especially if it is not exactly traditional.
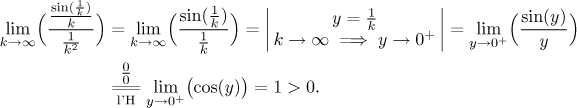
So our guess was correct and we can proceed with the comparison.
![]()
Since the test series on the right converges (see the p-test), so does the series on the left.
Conclusion: The given series converges.
We can get the same conclusion by the plain Comparison test, but we have to
tighten up on the estimate we tried before, it was too generous. We know
that for any positive y we have
![]()
and the conclusion follows from the fact that the larger test series converges.
Remark. Here we look closer at the integral from the Integral test. First, note that
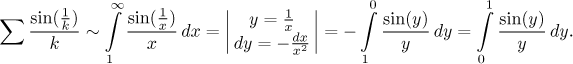
It is well-known that the function on the right does not have an antiderivative that can be expressed using elementary functions and operations. While this is the end of "classical" integration, we may try to approach this problem via power series. Using the standard expansion of sine we get
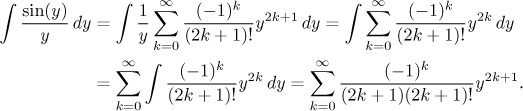
However, we can switch the integral and summation only on sets where the
series converges uniformly, see
Series of functions in Theory
- Series of functions. Fortunately for us, here we have
uniform convergence on the interval
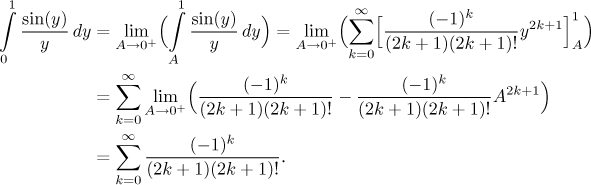
The resulting series is convergent, which is easy to show using the Alternating series test. So also the Integral test confirms that the given series converges, but it was so much trouble that the comparison approach is definitely better.